Drugs Methodology

Overview

Abstract

Substances, including drugs, gases, and hormones, are transported through the body within the bloodstream and airflow in the Cardiovascular and Respiratory Systems, respectively. This provides important nutrients and waste removal for normal physiologic function. The BioGears® engine models advection in both fluid systems (see Substance Transport Methodology). Transvascular transport is simulated using one of several diffusion models (see Tissue Methodology) for substances generically. Drug transvascular transport is modeled with a physiologically-based pharmacokinetic (PBPK) model, and the physiologic effects on the body are modeled with a low-fidelity pharmacodynamic (PD) model.

Introduction

Drugs influence the body by moving it out of homeostasis for a specific purpose, such as sedation for surgical intervention, or to address a patient condition, such as analgesic intervention. After a drug enters the patient’s body (through intravenous administration, absorption through the gastrointestinal system, or inhalation of an agent), the substance ultimately is transported through the bloodstream for uptake by the tissues and organs. The process of clearing a drug from the system is accomplished in a combination of three methods: renal clearance, hepatic clearance, and systemic clearance. Depending on the drug, it may be processed by either the kidney, the liver, or both for removal from the system as a waste product. Additionally, drugs are metabolized by the body and removed from the bloodstream. These methods all reduce the amount of drugs in the system. The drug transport and clearance methodologies in BioGears are described below.

System Design

Background and Scope

Pharmacokinetics is the study of the relationship between the dose of a drug and the time-evolution of the concentration of the drug throughout the body. The relationship between the concentration of a drug and the physiological response is described by the pharmacodynamics [293]. BioGears has both pharmacokinetic and pharmacodynamic models. Because it is physiologically-based, the pharmacokinetic model has resolution at the same scale as the cardiovascular and respiratory systems. Physiologically-based pharmacokinetic (PBPK) modeling is a technique that mathematically models the distribution, uptake, metabolism, and clearance of a drug with consideration of the relevant physiological processes [160]. The PBPK model provides more resolution than the classic one and two compartment models. The PBPK model also provides a base on which to build a receptor-based pharmacodynamic (PD) model, although the BioGears PD model is currently a lower-fidelity phenomenological model based solely on the concentration of a drug in the blood. Drugs impact body-level physiologic behavior such as heart rate, respiration rate, and blood pressure as result of cellular-level interactions caused by a drug that changes the behavior of physiologic entities, such as blood vessels and electrical activity in the heart. The cellular-level processes are not modeled in BioGears, and instead the PD model is a direct relationship between concentration and maximum effect for a body-level response.

Data Flow

Preprocess

Administer Substances and Administer IV Substances

All substances added or removed from the BioGears body are incremented or decremented from the appropriate compartment during the Preprocess step. For example, if substances are administered via a bolus injection or through intravenous administration, the substance mass is increased in the vena cava compartment.

Process

The generic substance methodology developed for the BioGears Engine is used to solve for the mass, concentration, substance volume, and volume fraction in each compartment. After the masses and concentrations have been updated, the system-level effects of any circulating drugs are calculated using the pharmacodynamic model.

Post Process

The Post Process step moves everything calculated in Process from the next time step calculation to the current time step calculation. Substances have no specific Post Process functionality. Each system post processes their circuit and moves the mass, concentration, substance volume, and volume fraction from next to current.

Figure 1. The data flow begins with a Preprocess step where substances entering or exiting the BioGears body are incremented or decremented. During the Process step, the mass and concentration (blood) or substance volume and volume fraction (air/gas) are calculated for each compartment in a system. During Process, the effects of any drugs in the system are calculated. There is no specific Post Process functionality in substances. However, as other systems post process their circuits, the substance values are moved from the next time step to the current time step calculation.

Features, Capabilities, and Dependencies

Pharmacokinetic models quantify the time evolution of drug distribution from the administration of a dose. Pharmacodynamic models, on the other hand, characterize the events from the arrival of the drug at the site of action to the “onset, magnitude and duration of the biological response" [293]. The BioGears Drug system contains both pharmacokinetic and pharmacodynamic models.

Pharmacokinetics

The pharmacokinetic (PK) methodology provides a means for simulating the time-evolution of the distribution of a drug throughout the body. This is accomplished by using the administration actions discussed in the Actions section below, the transport methodology, the perfusion limited diffusion methodology, and the substance files discussed in the Common Data Model documentation. Once a drug is administered, it either enters the Cardiovascular System (liquid) or the Respiratory System (inhaled). If it is an inhaled drug, modeled in BioGears as a gas, the drug will move into the alveoli through advection then diffuse into the Cardiovascular System through alveoli transfer. Drug effects, described below in the Pharmacodynamics section, are then computed based on the concentration of the drug in the plasma. Note that the plasma concentration calculation is currently incorrect. The concentration of a drug is currently computed by dividing the mass of the drug in a compartment by the volume of plasma, as computed from the hematocrit. Implicit in the plasma concentration calculation is the assumption that all of the drug is in the extracellular space. In actuality, some of the drug will cross blood-cell membranes, and the concentration of drug in the plasma and in the blood is a function of many factors, including the lipophilicity. We will address this error in the future.

Partition Coefficient

The drugs circulate around the cardiovascular circuit via the generic transport methodology described in the Circuit Methodology. However, drugs diffuse from the Cardiovascular System into the tissues via perfusion limited diffusion. For each drug, the physicochemical properties are used to calculate the partition coefficient. This partition coefficient describes the tendency of a particular drug to diffuse across the barrier between the cardiovascular and tissue spaces. Partition coefficients are calculated using physiochemical properties defined in the substance file associated with a drug. For a very weak base, an acid, or a neutral, Equation 1 is used to calculate the partition coefficient.

\[{K}_{pu} = f_{EW} + \frac{X * f_{IW}}{Y} + \frac{P * f_{NL} + (0.3 * P + 0.7) * f_{NP}}{Y} + \left[\left(\frac{1}{f_{u}} - 1 - \left(\frac{P * f_{NL} + (0.3 * P + 0.7) * f_{NP}}{Y}\right)\right) * \frac{PR_{T}}{PR_{B}}\right] \]

Equation 1.

For moderate to strong bases, Equation 2 is used to calculate the partition coefficient.

\[{K}_{pu} = f_{EW} + \frac{1 + 10^{pK_{a}-pH_{IW}} * f_{IW}}{1 + 10^{pK_{a}-pH_{p}}} + \frac{K_{a}*AP_T*10^{pK_{a}-pH_{IW}}}{1+10^{pK_{a}-pH_{p}}} + \frac{P * f_{NL} + (0.3 * P + 0.7) * f_{NP}}{1+10^{pK_{a}-pH_{p}}}\]

Equation 2.

Where X and Y are the different relationships for pH, as shown in Table 1, f_IW is the fraction of intracellular water, f_EW is the fraction of extracellular water, f_NP is the fraction of neutral phospholipids in the tissue, f_NL is the fraction of lipids in the tissue, P is the octanol:water partition coefficient for the drug, f_u is the fraction of the drug unbound in plasma, f_NL,P is the fraction of neutral lipids in plasma, f_NP,P is the fraction of phospholipids in plasma, and PR_T / PR_B is the tissue to plasma ratio of the binding protein.

Table 1. The pH effects on the partition coefficient are described based on the drug type, i.e., very weak base, acid, or neutral. X relates the drug property pK_a to the pH_IW, intracellular water pH, while Y relates the pK_a to the pH of the plasma.

Ionic State	X	Y
Acid	\[1 + 10^{pH_{IW}-pK_{a}}\]	\[1 + 10^{pH_{p}-pK_{a}}\]
Very Weak Base	\[1 + 10^{pK_{a}-pH_{IW}}\]	\[1 + 10^{pK_{a}-pH_{p}}\]
Neutral	1	1

A number of these values are drug parameters found in the substance file definitions. However, many of them are organ/compartment dependent as shown in Tables 2 and 3.

Table 2. The volume fractions for neutral lipids and phospholipids vary by compartment. These values are specified for each compartment as outlined below and used to calculate the partition coefficient of each drug for each tissue compartment in the BioGears engine. These values were found in [287].

Tissue Compartment	Extracellular Water (fEW)	Intracellular Water (fIW)	Neutral Lipd (fNL)	Neutral Phospholipid (fNP)
Adipose (Fat)	0.135	0.017	0.853	0.0016
Bone	0.1	0.346	0.017	0.0017
Brain	0.162	0.620	0.039	0.0015
Gut	0.282	0.475	0.038	0.0125
Kidney	0.273	0.483	0.012	0.2420
Liver	0.161	0.573	0.014	0.2400
Lung	0.336	0.446	0.022	0.0128
Muscle	0.118	0.630	0.010	0.0072
Myocardium	0.320	0.456	0.014	0.0111
Skin	0.382	0.291	0.060	0.0044
Spleen	0.207	0.579	0.0077	0.0113

Table 3. The tissue to plasma protein binding ratios are shown for each tissue compartment in the BioGears Engine. Two proteins are available for drug binding, albumin and lipoprotein. The binding protein for each drug is specified in the substance file. These values were found in [287].

Tissue Compartment	Tissue to Plasma Albumin Ratio	Tissue to Plasma Lipoprotein Ratio
Adipose (Fat)	0.049	0.068
Bone	0.100	0.050
Brain	0.048	0.041
Gut	0.158	0.0141
Kidney	0.130	0.137
Liver	0.086	0.161
Lung	0.212	0.168
Muscle	0.064	0.059
Myocardium	0.157	0.160
Skin	0.277	0.096
Spleen	0.097	0.207

The BioGears implementation of the partition coefficients calculation and all values shown in the tables are derived from the literature [287] [286] [160] [149] [374].

If it is not possible to obtain the information required to compute the partition coefficient for a drug, or if the calculation is not valid for a particular drug for any reason, it is possible to override the computation by directly inputting a constant partition coefficient in the drug file. Note that, to use this functionality, it is best to input a coefficient for every tissue compartment in the model. BioGears currently uses the coefficient-computation override methodology for Albuterol, Ketamine, Morphine, and Sarin. The parameters used to calculate each partition coefficient were found in published data and/or tuned to get the desired kinetic response.

Diffusion

The above partition coefficients are used to calculate the diffusion of a drug across the tissue-vascular barrier. All current drugs in the BioGears Engine use perfusion limited diffusion as found in [160] [149]. For details on perfusion-limited and other diffusion modalities, see the Tissue Methodology.

In the current version of BioGears, all drugs diffuse by the perfusion-limited model described above. An alternative means for modeling drug kinetics would be to leverage the other diffusion methods described in the Tissue Methodology report. The other diffusion models were developed primarily for the transmembrane transport of ions and a few specific organic molecules (e.g. glucose), and they have not been tested for drugs.

Clearance

The PBPK model represents renal, hepatic, and systemic clearance. The renal clearance rate, intrinsic clearance rate, and the systemic clearance rate are specified in the substance file in units of milliliter-blood per second per kilogram. The intrinsic clearance rate is used to calculate the hepatic clearance, as shown in Equation 3.

\[Cl_{H} = \frac{Q_{H}*f_{u}*Cl_{I}*BW}{Q_{H} + f_{u}*Cl_{I}*BW} \]

Equation 3.

Where Cl_H is the hepatic clearance, f_u is the fraction of the drug unbound in plasma, Cl_I is the intrinsic clearance, and BW is the patient body weight.

The amount of drug removed (cleared) from the system is found by calculating the amount of fluid volume that can be cleared by a healthy organ. The volume is calculated, as shown in Equation 4. This process is completed for the renal and hepatic clearance.

\[V_{Cl} = Cl_{H}*BW*dt \]

Equation 4.

Where V_cl is the volume cleared, Cl_H is the organ clearance rate, BW is the body weight, and dt is the time step. The actual mass of the substance removed during this process is found by determining the amount of the drug in the volume cleared, as shown in Equation 5.

\[M_{Cl} = V_{Cl}*C \]

Equation 5.

Where M_Cl is the mass cleared, V_Cl is the volume cleared, and C is the concentration in the tissue. The systemic clearance represents the total clearance for the body, including the renal and hepatic clearance. Therefore, the total volume cleared is calculated, then the renal and hepatic clearance volumes are removed, as shown in Equation 6. The “remaining” systemic mass cleared is calculated as shown in Equation 5. Half of the mass cleared from renal clearance is removed from each of the kidney tissue compartments, the mass cleared from hepatic clearance is removed from the liver tissue compartment, and the mass removed from the “remaining” systemic clearance is removed from the vena cava compartment. This is assumed to be from various metabolic processes in the plasma.

\[V_{Cl} = \left(Cl_{s}*BW*dt\right) - V_{ClR} - V_{ClH} \]

Equation 6.

Where V_Cl is the remaining systemic volume cleared, Cl_S is the systemic clearance rate, BW is the patient body weight, dt is the time step, V_ClR is the renal volume cleared, and V_ClH is the hepatic volume cleared.

Pharmacodynamics

Pharmacodynamic (PD) models characterize the effect that a drug has on the organism. The current version of BioGears contains two pharmacodynamic models.

• A simple dose-response model with a response biomarker functionally linked to the plasma concentration of a drug via a first order rate constant.
• A site-of-action model with a local response functionally linked to the local tissue concentration of a drug

Effect Site Model

Development of the BioGears pharmaocodynamic model began with a characterization of expected results by subject matter experts for a small library of drugs. The expected results were limited to whole-body biomarkers similar to vital signs (e.g. changes in heart rate, respiration rate, blood pressure, etc.). We treated the expected results as surrogate endpoints and used the common sigmoidal E_max model to characterize the effects. The model was initially calibrated to drug plasma concentration but has been updated to account for delays in equilibration between the concentration in the plasma and at the site-of-action. This was accomplished by introducing a hypothetical "effect site" compartment, transfer to which from the plasma is governed by a drug-specific first order rate constant (k_e) [191]. The utility of this strategy is evident when considering a drug such as morphine, which exhibits delays in pharmacological activity due to its slow diffusion across the blood-brain barrier to the central nervous system, where it primarily targets mu-opioid receptors [190]. In the case of drugs for which k_e data was not available, the effect site concentration is assumed to be the plasma concentration as before.

In its first iteration, the E_max model referred to the expected effect of the drug rather than the maximum effect of the drug. For that reason, overdose modeling is not possible for most drugs in BioGears. We are working to obtain empirical data from case studies that will allow us to adjust drug response curves to describe non-clinical dose regimes. Currently, only morphine has been completed with satisfactory overdose functionality (see Opioid Intoxication). The pharmacodynamic effects included in the BioGears effect concentration PD model are described in Table 4.

Table 4. Pharmacodynamic effects modeled in the BioGears Engine with descriptions and relevant ranges.

Pharmacodynamic Effect	Description	Available Values
Bronchodilation	Drug effect on the bronchii radii. A maximal effect of 1.0 will reverse the constriction of an asthma attack.	0 to 1
Diastolic Pressure	Change in the diastolic pressure. Given as a fraction.	-1 to 1
Heart Rate	Change in the heart rate. Given as a fraction.	-1 to 1
Hemorrhage Flow	Change in hemorrhage bleeding rate, with negative reducing the effect of hemorrhage.	-1 to 1
Neuromuscular Block	Drug’s strength as a neuromuscular block, with a 1.0 as the strongest block.	0 to 1
Pupil Size Modifier	Drug effect on the pupil diameter. Given as a modifier.	-1 to 1
Pupil Reactivity Modifier	Drug effect on the pupil reactivity to light. Given as a modifier.	-1 to 1
Respiration Rate	Change in the respiration rate. Given as a fraction.	-1 to 1
Sedation	Drug’s strength as a sedative, with a 1.0 as the strongest sedative.	0 to 1
Systolic Pressure	Change in the systolic pressure. Given as a fraction.	-1 to 1
Tidal Volume	Change in the tidal volume. Given as a fraction.	-1 to 1
Tubular Permeability	Drug localized effect on tubulear permeability. Given as a severity, 1.0 complete reabsorption block	0 to 1
Central Nervous Response	Drug depressant effect on receptors in the central nervous system directing chemoreceptor action. Given as a severity with 1.0 being complete suppression	0 to 1

The drug effects are specified for each drug in the substance file. The level of effect is calculated based on the expected effect (or, for some drugs, the maximum effect) of the drug and the current effect site concentration for the drug, as shown in Equation 7 [225] and Equation 8 [293].

\[\frac{dC_{e}}{dt} = k_{e}*(C_{p}-C_{e}) \]

.

Equation 7.

\[\Delta E = E_{bl}*\frac{E_{m}*C_{e}^\eta}{EC_{50}^\eta+C_{e}^\eta} \]

Equation 8.

According to Equation 7, the rate at which the effect compartment concentration (C_e) equilibrates with the plasma concentration (C_p) is directly proportional to the difference between (C_p) and (C_e) and a first order rate constant, k_e. Note that it is assumed that the rates of influx to and efflux from the effect compartment are equivalent. (C_e) is utilized in Equation 8, where E_m is the expected (or maximum) effect of the drug, EC₅₀ is the concentration at 50% of the effect, E_bl is the baseline for that effect (i.e., heart rate baseline), ΔE is the calculated effect of the drug, and η is the slope factor [293]. This procedure is repeated for each of the effects in Table 4.

The drug effect is applied as a fraction of the baseline for the biomarker, which is a patient variable in BioGears. For example, a person with a resting heart rate of 72 bpm may have a physiological process happening during simulation, perhaps as a condition, which increases his/her baseline heart rate to 80 bpm. If this patient is given a drug with a heart rate effect of 0.2, then at maximum the patient's heart rate will be 96 bpm (80 + 0.2 * 80). If the same drug were given to the same patient but without the condition, the maximum heart rate will be 86.4 bpm (72 + 0.2 * 72).

The EC₅₀ values which could not be inferred from literature were estimated from the maximum concentration of the drug at a standard adult dose, as shown in Equation 9.

\[EC_{50} = \frac{C_{max}}{32} \]

Equation 9.

Where C_max is the maximum plasma concentration for the standard adult dose and EC₅₀ is the concentration at which 50% of the effect should be present.

Drug-Drug Interactions

Drugs can be administered in combination in BioGears. However, in most cases the interaction will modeled only by stacking the pharmacodynamic modifiers associated with each drug. Such an approach is appropriate in very limited circumstances. We currently have two reversal agents whose interactions with their targets are modeled in greater detail: Pralidoxime–an organophosphate antagonist (see Sarin Model)–and naloxone, which opposes opioids such as Morphine and Fentanyl. Naloxone is an interesting case because it exerts virtually no pharmacodynamic effects on its own; it operates solely by competitively binding with opioids for mu receptors in the central nervous system [122]. The impact of competitive antagonists on the effect of an agonist such as an opioid can be modeled by Equation 10 [44].

\[\Delta E = E_{bl}*\frac{E_{m}*C_{e}^\eta}{EC_{50}^\eta*(1+\frac{C_I}{K_I})^\eta+C_{e}^\eta}\]

Equation 10.

The parameters E_bl, E_m, C_e, and EC₅₀ are defined as previously with respect to the agonist. K_I captures the tendency of the antagonist to displace the agonist from the shared target receptor (lower implies greater potency). Conveniently, when no antagonist is present, Equation 10 reduces to Equation 8, allowing it to be implemented with minimal additional modeling effort. Naloxone reversal of opiod induced respiratory depression is currently the only competitive antagonism scenario modeled in this way (see Reversal of Opioid Induced Respiratory Depression). We are working to incorporate partial and non-competitive antagonism, which will allow us to describe increasingly complex interactions.

Cardiovascular Effects

Equation 8 provides a straightforward calculation for the heart rate. However, to be applied in the cardiovascular system, the drug effects need to be translated to the effects on the mean arterial pressure and the pulse pressure. This is accomplished using Equations 11 and 12. These equations were developed using the relationship between diastolic and systolic pressure and the mean arterial pressure [134].

\[\Delta MAP = \left(2* \Delta DBP \right) + \frac{\Delta SBP}{3} \]

Equation 11.

\[\Delta P_{pulse} = \Delta SBP - \Delta DBP \]

Equation 12.

Where MAP is the mean arterial blood pressure, DBP is the diastolic blood pressure, and SBP is the systolic blood pressure. These changes to the heart rate, mean arterial pressure, and pulse pressure are then system outputs for the drug system. The changes are then applied in the Cardiovascular System. For more details on the implementation of the effects see the Cardiovascular Methodology.

Respiratory Effects

As with the Cardiovascular System, the respiratory and tidal volume effects are relatively straight forward to apply. The neuromuscular block and sedation levels are calculated to have an effect level between zero and one, where zero is no effect and one is a maximal effect. The detail of how these are implemented can be found in the Respiratory Methodology.

Site-of-Action Models

There are currently three drugs which utilize a localized PD effects model: Albuterol, Furosemide, and Sarin.

Respiratory Effects

Aerosolized substances have a direct effect on the respiratory system. There are two direct-effect aerosol substance properties.

• BronchioleModifier
  • A parameter which controls the dilation (positive value) or constriction (negative value) of the bronchioles in the presence of the substance
• InflammationCoefficient
  • A parameter to quantify the propensity of the aerosol to cause inflammation of the respiratory tissues

For example, Albuterol is an aerosolized drug that typically enters the body via nebulizer or metered-dose inhaler. Accordingly, in BioGears Albuterol enters the body through the respiratory tract and diffuses into the respiratory tissues (see the Aerosol Section in the Environment Methodology report). The BronchioleModifier for Albuterol is set to 1 in the substance file, meaning that Albuterol has the capability to maximally dilate the bronchioles. The bronchodilatory effects of Albuterol are applied directly at the site of action, and the actual bronchodilation is a function of the concentration of Albuterol in the respiratory tissues. The nerve agent Sarin has the opposite effect of Albuterol, inducing severe bronchoconstriction. As such, the BronchioleModifier for Sarin is set to a negative value. See the Nerve Agent: Sarin section for more details.

Renal Effects

The pharmacodynamic effects of diuretics locally target the renal system's functionality. Local binding of the Na-K-2Cl symporter by Furosemide (Lasix) in the tubular lumen stimulates an increase in urine production and ion excretion. In BioGears we simulate this effect by adjusting the reabsorption permeability as a function of plasma concentration of Furosemide. This enables simulation of the whole-body drug effects, but the model does not use the local concentration of drug in the tubular lumen as the primary determinant of the reabsorption adjustment. A mechanistic model based on traditional receptor theory which combines the tissue properties of receptor concentration and signal transduction with the drug properties of intrinsic efficacy and affinity to form a model of drug response would use the local tissue concentration as the first link in a causal chain leading to permeability changes and the appropriate downstream effects. This type of mechanistic model is recommended as future work. For details on the reabsorption and urine production of the renal system, see the Renal Methodology report. The results of the Lasix administration simulation are compared to data found in literature and presented in the validation section.

Substances

The full list of drugs available in the BioGears library can be found in Table 5 in the Validation section. Additional substances, such as oxygen, carbon dioxide, and hemoglobin that are available in the BioGears Engine can be found in the Blood Chemistry Methodology.

Compounds

BioGears compounds allow a user to administer a specific combination of substances (see above) at the same time. In most cases, compounds (or solutions) used in BioGears can be represented by their ionic components.c Currently, BioGears supports the following compounds:

• Piperacillin TazobactamL A combination of piperacillin, tazobactam, and sodium.
• Plasma: Plasma contains components similar to whole blood but without any blood cells. The plasma compound contains sodium, albumin, urea, glucose, triacylglycerol, calcium, creatinine, chloride, and potassium.
• Plasma Lyte A: A buffered solution made up of sodium, potassium, magnesium, chloride, acetoacetate, and glucose.
• Ringers Lactate: A sodium lactate solution consisting of sodium, chloride, lactate, potassium, calcium, oxygen, carbon dioxide.
• Saline: A combination of sodium, chloride, oxygen, and carbon dioxide.
• Whole Blood: BioGears supports all eight primary blood types (A, B, AB, and O each either Rh positive or negative). Each whole blood compound contains hemoglobin, oxyhemoglobin, oxygen, carbon dioxide, sodium, albumin, urea, glucose, triacylglycerol, calcium, creatinine, chloride, potassium, red blood cells, white blood cells, platelets, and the appropriate antigens corresponding to blood type.

Patient Variability

It is possible to customize the body that is simulated by BioGears. For a detailed discussion of patient variability in BioGears please see the Patient Methodology report. Variability in body morphology will obviously have an effect on the pharmacokinetics of a drug. For example, a larger body may have a larger plasma volume, and thus the plasma concentration for a specific dose of a drug will be less than the same dose administered to a smaller body. Additionally, the partitioning of drugs is dependent on the relative masses of the physiological compartments, and storage is affected by distribution. Lipophilic drugs may appear to remain longer in the BioGears plasma in patients who are configured with a higher body fat fraction. Patient configuration will also impact the pharmacodynamics. Maximum drug effects are computed as a fraction of baseline physiology. Changing a patient's baseline parameter (e.g. heart rate baseline) will also change the maximum effect (e.g. maximum heart rate) at a specific concentration of a drug. All drug validation is performed on a BioGears Standard Male.

Dependencies

The substance calculations rely on the flow values calculated by the Circuit Methodology to calculate the movement of substances from compartment to compartment in each circuit. Any limitations and assumptions associated with this methodology will also be associated with the Drugs Methodology. The pharmocokinetic modeling is reliant on accurate values for the physical chemical properties of drugs. If these parameters are unknown or estimated from animal studies, the calculation for the partition coefficient may become unreliable. For some drugs, this information may be difficult to determine. The BioGears model also allows the user to supply partition coefficients directly. Some third party resources, both open source and commercially available, may provide this data for users, allowing incorporation of the data into the BioGears full body simulation.

While this model is primarily used for drugs, it could be used for any substance in the body. BioGears uses the clearance methodology for several additional substances. The modular approach to these calculations allows for the use of any combination of the three methodologies, PK, clearance, and PD.

The substance values and calculations are used by a variety of systems to trigger actions and responses, define physiologic set points, scale circuit parameters, and modify driver frequencies. Many of these triggers and responses are discussed in the Blood Chemistry Methodology and the Endocrine Methodology. The drug-specific effects are listed and described briefly in Table 5. The implementation of these calculated responses can be found in the Cardiovascular Methodology and the Respiratory Methodology.

Assumptions and Limitations

The Drugs Methodology is based on the assumption that all substances are suspended in the fluid (blood or air, depending on the system) and move through the circuits with the flow. While this does allow for renal and hepatic clearance and metabolic elimination of substances, it does not allow for particle deposition. This assumption is valid for the level of fidelity of the model. In the future, particle deposition can be addressed by adding a more detailed substance methodology with factors for deposition within an organ, tissue, or blood vessel. Also, not included is a method for modeling vaporized substances, such as albuterol. In the future, we will add this methodology to allow a liquid in the respiratory tract and produce a more realistic representation of the behavior.

The drug model addresses many of the earlier limitation of the BioGears drug model. This includes creating a substance file that uses physiochemical properties to define the pharmacokinetic properties and intuitive modifiers to calculate the pharmacodynamic effects. However, this implementation of a PD model works best with a drug with immediate effects, such as anesthesia medications. This implementation has not been tested for drugs with a later onset due to secondary mechanisms. This is an area for future work. Additionally, no drug interactions or intoxication is modeled.

Actions

Interventions

Bolus Administration

A bolus administration represents an injection of a substance in a single dose. The substance, concentration, and amount are specified by the user. The total mass for the dose is calculated by multiplying the concentration and the amount. The total mass is then incrementally added to the vena cava compartment over the course of two seconds to represent the slow depression of a plunger. Once added to the vena cava, the substance will circulate through the Cardiovascular System as part of the blood flow. The effects of the substance on the physiologic output will vary with the substance.

IV Administration

Intravenous administration represents administration of a compound substance (a single entity with multiple substances, i.e., saline) at a specified rate over time into the venous system. The compound substance, the rate, and the bag volume are specified by the user. At each time step, the mass of the substances are incremented based on the amount of compound substance entering the system. The mass is calculated by taking the flow entering the system at each time step multiplied by the known concentration of each substance within the compound substance. This mass is then added to the vena cava at each time step until the intravenous administration is stopped. The added substances will then circulate through the Cardiovascular System as part of the blood flow. The effect on the physiologic output will vary based on the compound substance selected.

IV Infusion

Titration represents the administration of a single substance at a specified rate and concentration over time into the venous system. The user selects a single substance and specifies the concentration and rate with titration. As with intravenous administration, the mass of the substance is incremented based on the amount of the substance entering the system. The mass is calculated by taking the flow entering the system at each time step multiplied by the known concentration of each substance within the compound substance. This mass is then added to the vena cava at each time step until the intravenous administration is stopped. The added substances then circulate through the Cardiovascular System as part of the blood flow. The effect on the physiologic output will vary based on the compound substance selected.

Oral (Gastrointestinal)

Drugs administered orally are transported to the bloodstream via an advanced compartment and transit (ACAT) model. Examples of ACAT models with varying numbers of compartments are plentiful in the literature; the BioGears implementation follows the work of [406] and [7]. The gastrointestinal track is divided into nine regions in which both solid and dissolved drug concentrations are tracked: Stomach, Duodenum, Jejunum 1, Jejunum 2, Ileum 1, Ileum 2, Ileum 3, Cecum, and Ascending Colon. The rate of mass transit between compartments is governed by first order rate constants defined in [406], while the rate of drug dissolution within each compartment is determined by the Noyes-Whitney equation [406]. Every compartment except the stomach exchanges dissolved drug mass via permeation with an enterocyte layer from which drug is deposited in the portal vein. The rate of permeation from each region depends on the local pH and drug-specific parameters (LogP, pKa, molecular weight, polar surface area, number of hydrogen bonds) as outlined in [399].

Oral (Transmucosal)

BioGears has develeloped a specialized model for administration of oral transmucosal fentanyl citrate (OTFC). Fentanyl is deposited as a solid in the mouth and its rate of dissolution is calculated via the Noyes-Whiney equation. Dissolved fentanyl diffuses through the oral mucosal layer into the systemic circulation. We solve the diffusion equation by discretizing the oral mucosal barrier into thin layers and applying a central finite difference strategy. The physical properties of the mucosal layer (surface area, thickness) were obtained from [404] [414] [309]. A large fraction of the dissolved fentanyl is swallowed and enters the stomach compartment of the ACAT model described above, after which it is subjected to first-pass metabolism. In this way, approxiamtely 50% of the fentanyl reaches the systemic circulation, which is in line with observations in pharmacokinetic studies [346] [341].

Results and Conclusions

Validation - Resting Physiologic State

The Drugs Methodology has no resting state validation.

Validation - Actions

Bolus Administration

All drugs in the BioGears library were validated qualitatively or with subject matter expert input. The bolus injection methodology was validated by comparing the PK and PD results to literature. See the sections below for more detail.

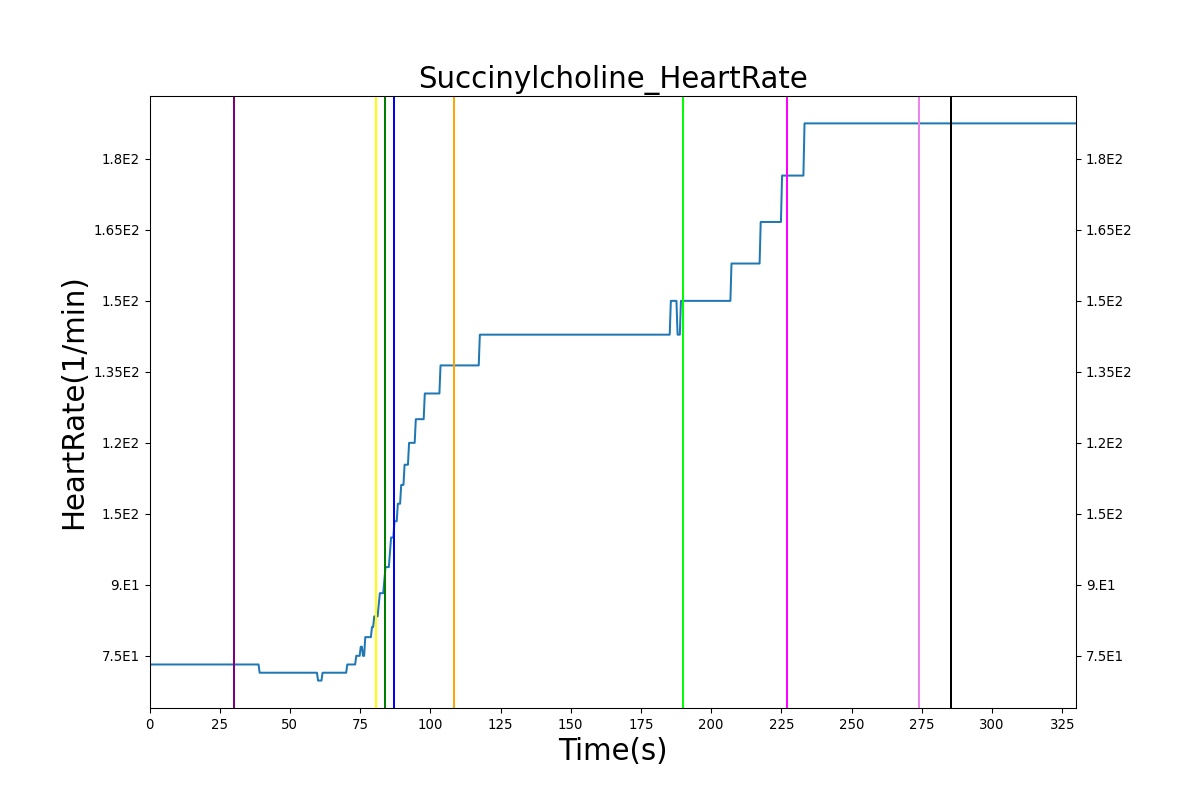
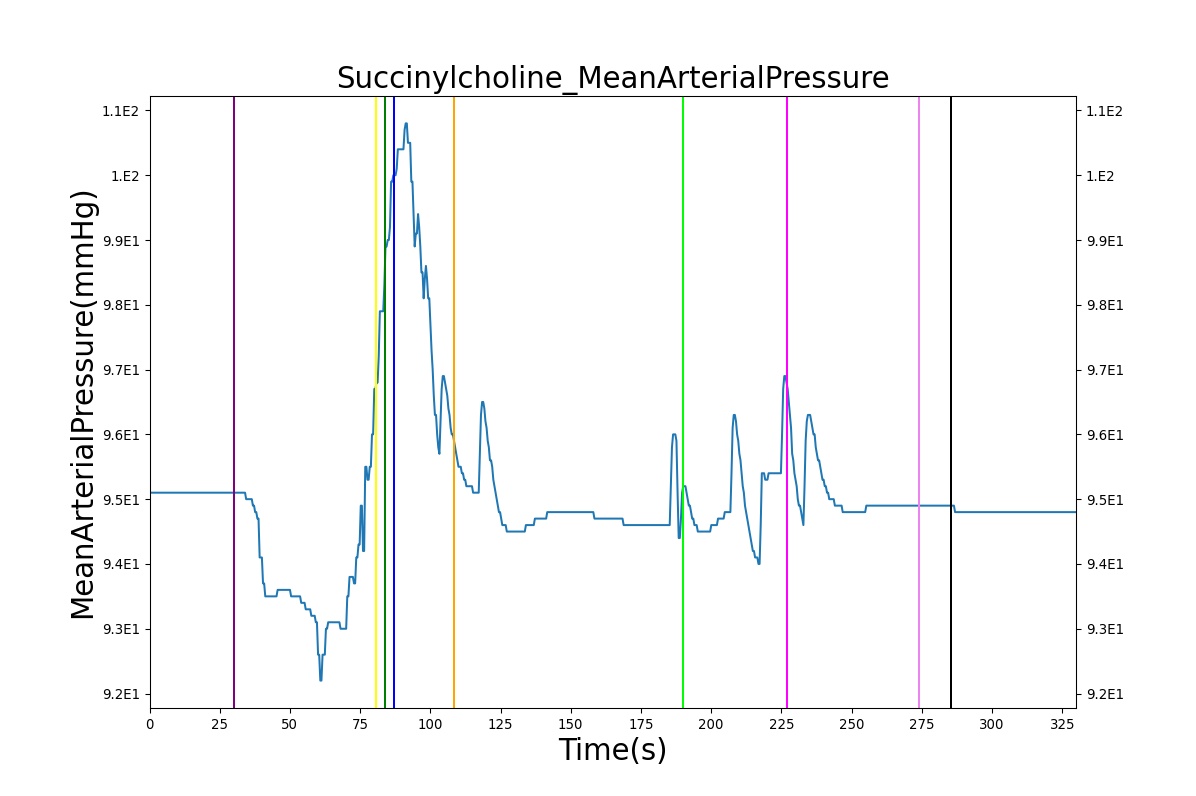
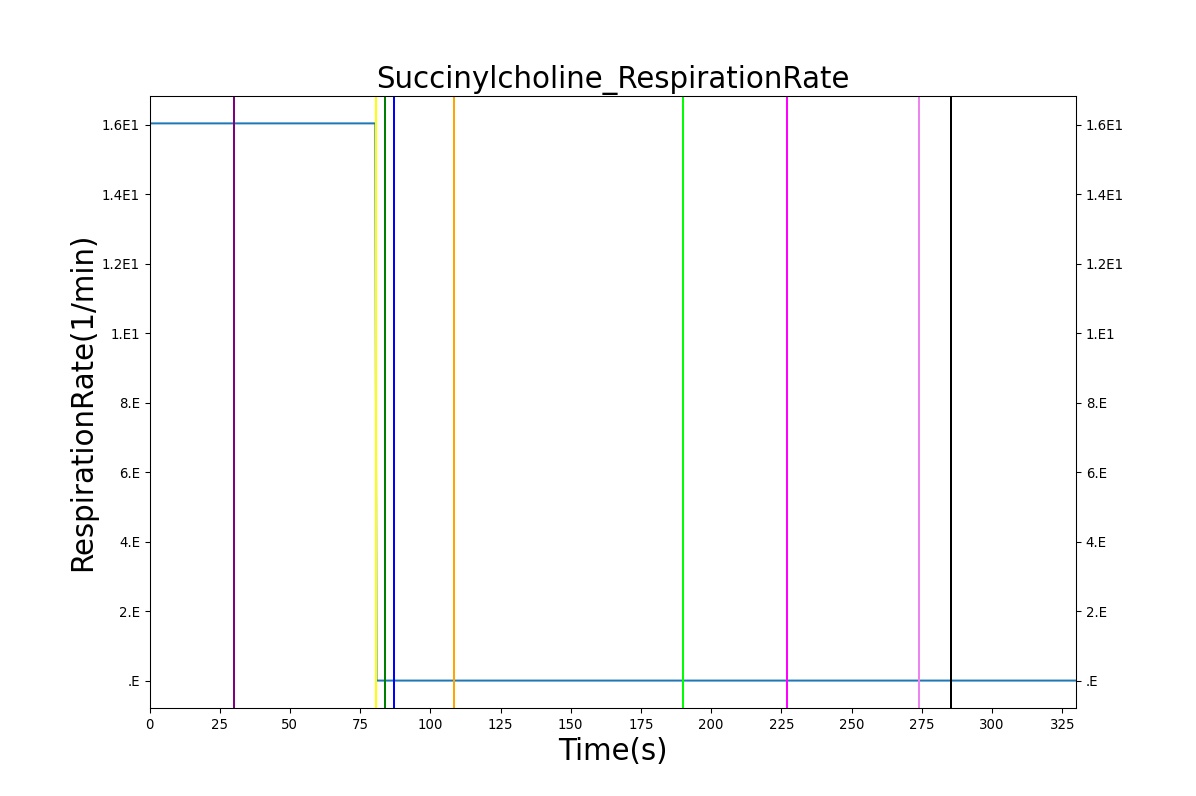
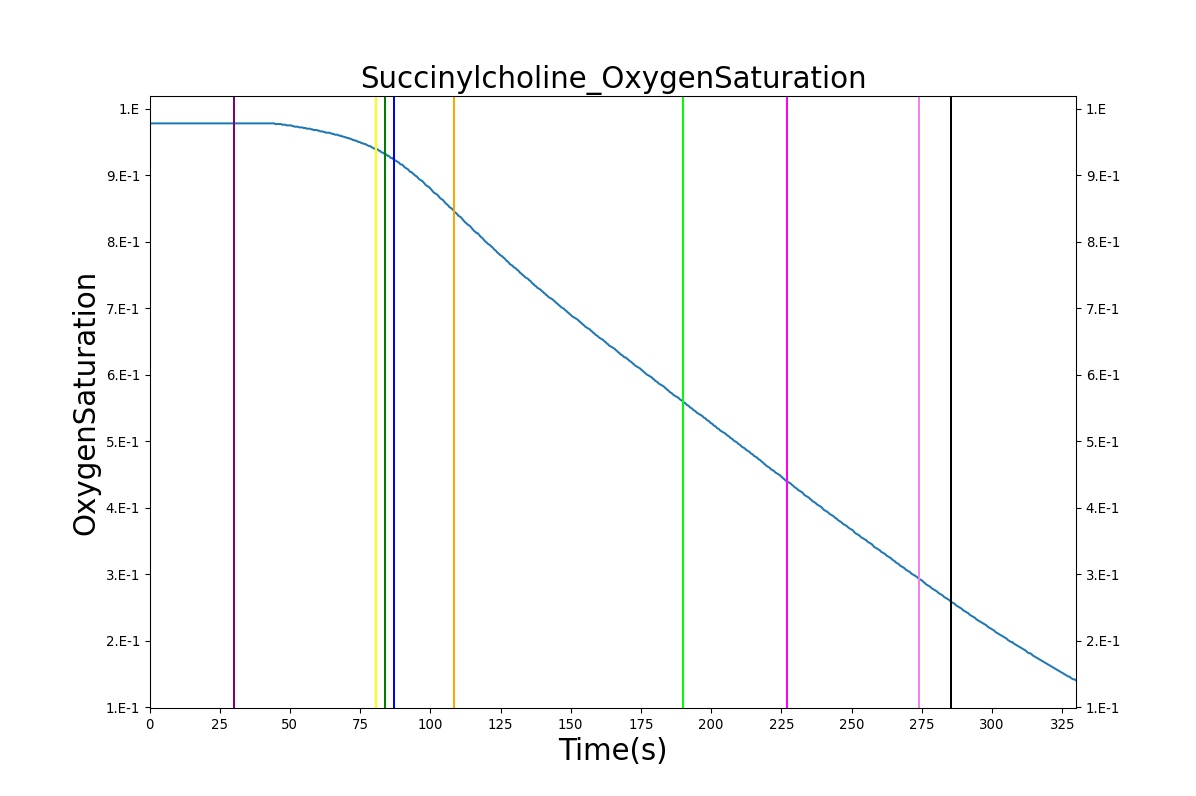
The Succinylcholine scenario shows a drug impacting the major BioGears systems. Succinylcholine (Figure 2) initially drops the heart rate and blood pressure approximately 5–10%. As expected, the respiration drops to zero within 60–90 seconds to represent the paralysis associated with the neuromuscular blocker. The oxygen saturation drops slowly as the concentration of oxygen in the bloodstream drops, leading to hypoxia. Epinephrine is released in response to hypoxia, causing an increase in heart rate and blood pressure (Endocrine Methodology). This is an example of the interdependent nature of the BioGears systems and the chain reaction drug administration can cause.

Figure 2. The neuromuscular blocker, Succinylcholine, causes a cessation of respiration due to its paralytic effects. The heart rate and blood pressure initially decrease due to the system-level drug effects. As the oxygen decreases, hypoxia occurs, resulting in an increase in heart rate and blood pressure.

Intravenous Administration

Validation of intravenous administration of a hypotonic solution and blood products can be found in the Cardiovascular Methodology.

Validation - Pharmacokinetic

The PK model was validated by comparing the plasma concentration calculated by the BioGears Engine to plasma concentration curves found in the literature. The comparisons are shown in Figures 3–17. No available data was found for Epinephrine, so this drug was only validated from a PD perspective.

Figure 3. Albuterol is an aerosol, but it is modeled as a gas in BioGears. Alveolar exchange takes place bidirectionally as long as the "gas" (aerosol) is in the blood or in the environment. For that reason, the concentration of Albuterol in the plasma diminishes much faster in BioGears than demonstrated in literature [9]. This is a known issue and an area of future work for BioGears.

Figure 4. The kinetics of inhaled anesthetics like desflurane are generally described by the end tidal fraction of the anesthetic [107]. Validation data assumes an inspired concentration of 5% desflurane administered for 30 minutes [192] followed by a two hour wash out time [408]. BioGears accurately captures the speed of wash-in but underestimates the speed with which desflurane washes out.

Figure 5. The physical chemical properties of fentanyl found in the literature were used to produce a good fit for the plasma concentration. The experimental data was found in [316].

Figure 6. The physical chemical properties of furosemide found in the literature were used to produce a good fit for the plasma concentration. The experimental data was found in [139].

Figure 7. The partition coefficients were calculated from initial physical chemical properties found for Ketamine. However, the fit was unsatisfactory, so the partition coefficients were directly estimated for this drug to produce a good fit with the plasma concentration curve found in [405].

Figure 8. The BioGears curve for midazolam plasma concentration shows a good overall fit with the experimental data found in [313]. However, the clearance dominant (end) portion of the curve shows that BioGears should be clearing more quickly, while midazolam appears to move into the tissues too quickly during the diffusion dominant portion of the curve (beginning).

Figure 9. The partition coefficients for morphine estimated in [83] were used in lieu of those estimated using physiochemical data. Doing so provided a better fit to the experimental data found in [190].

Figure 10. The partition coefficients were calculated from initial physical chemical properties found for Naloxone. They produce a good fit with the plasma concentration curve found in [3].

Figure 11. The pralidoxime experimental data found in [1] was collected after an intramuscular injection. This administration method is available in BioGears, so was used to validate the drug. The overall fit between the BioGears data and the experimental data was good. A slightly higher concentration throughout was evident and may be attributed to the amount of drug that never exits the muscle when this type of injection occurs. In the future, a loss factor could be added to represent this drug amount.

Figure 12. The physical chemical properties of prednisone found in the literature were used to produce a good fit for the plasma concentration. The experimental data was found in [291].

Figure 13. The propofol experimental data was collected during and after an infusion of propofol. BioGears is able to support a rate and concentration input for an infusion; therefore, the infusion methodology was used to adminster propofol in the engine. The infusion explains the initial curve evident in the plasma concentration. The initial diffusion dominant portion of the curve shows a reduced diffusion into the tissues compared to the experimental data; however, the clearance dominant portion of the curve shows good agreement with the data found in [384].

Figure 14. The BioGears calculated plasma concentration curve for Rocuronium shows good agreement with the experimental data found in [65]. This is particularly true for the diffusion dominant portion of the curve, while the BioGears clearance is less than that shown in the experimental data.

Figure 15. Pharmacokinetic data for Sarin inhalation is non-existent with respect to humans and in short supply with respect to animals. Most animal studies administer Sarin either orally or intravenously. The data above was obtained from a study in which guinea pigs inhaled a potentially lethal dose of Soman (another organophosphate nerve agent) [24]. The BioGears simulation assumes a 6-minute exposure to Sarin aerosol at a concentration of 15 mg/m³. These results indicate reasonable uptake and diffusion of Sarin via the lungs.

Figure 16. The succinylcholine pharmacokinetics were initially calculated from the values found in literature for the physical chemical properties. However, this was significantly adjusted to attempt to match the calculated plasma concentration to the experimental data found in [298].

Figure 17. The TXA pharmacokinetics were initially calculated using physiochemical propertioes found in literature with slight adjustments made over time to allow for BioGears plasma concentration to account for proper clearance [238]

Figure 18. Vasopressin is naturally produced in the body, but the dose given here is much greater than basal levels so this should not be a confounding factor. The predicted values are generally in agreement with the data reported in [118]

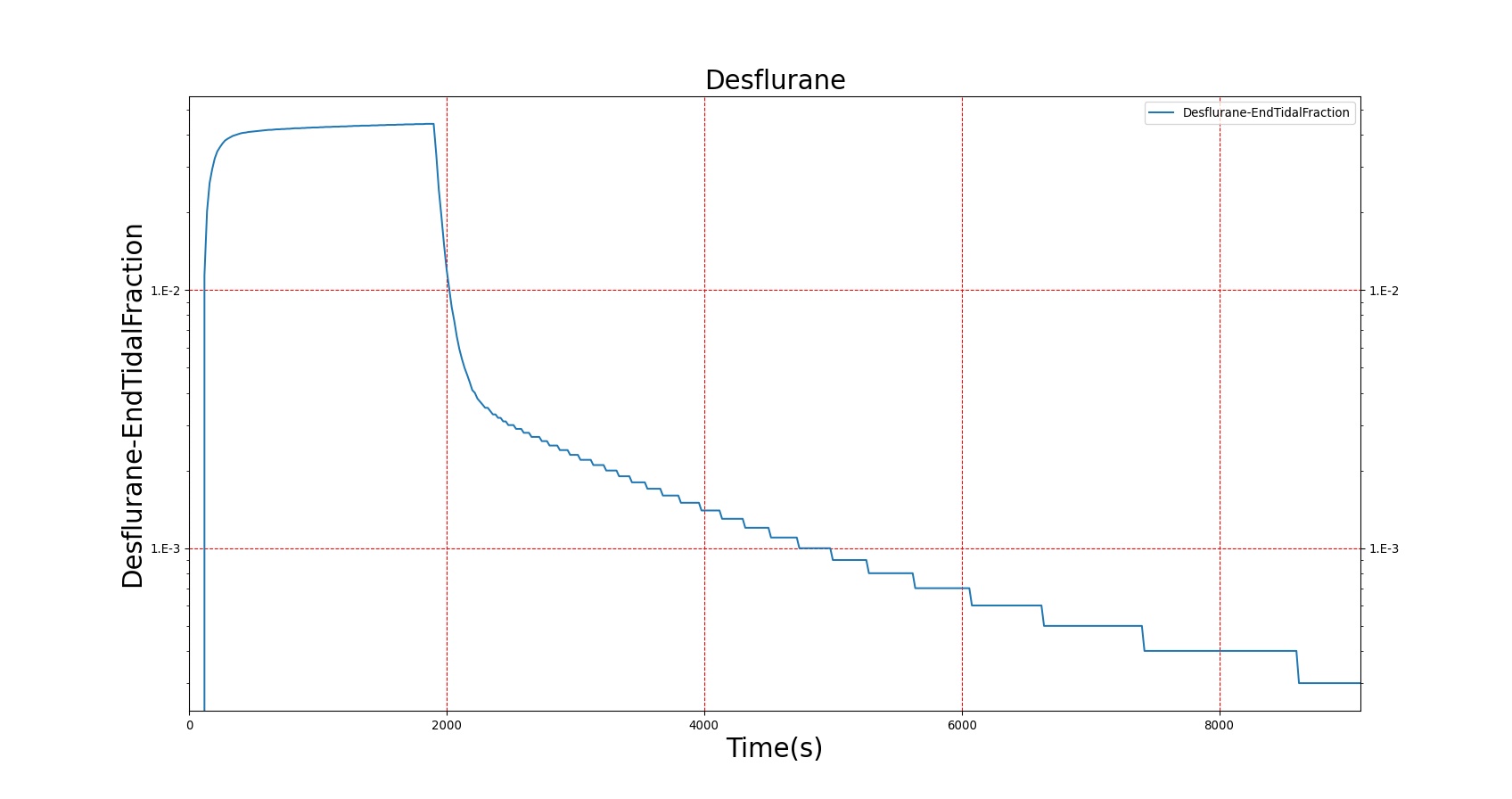
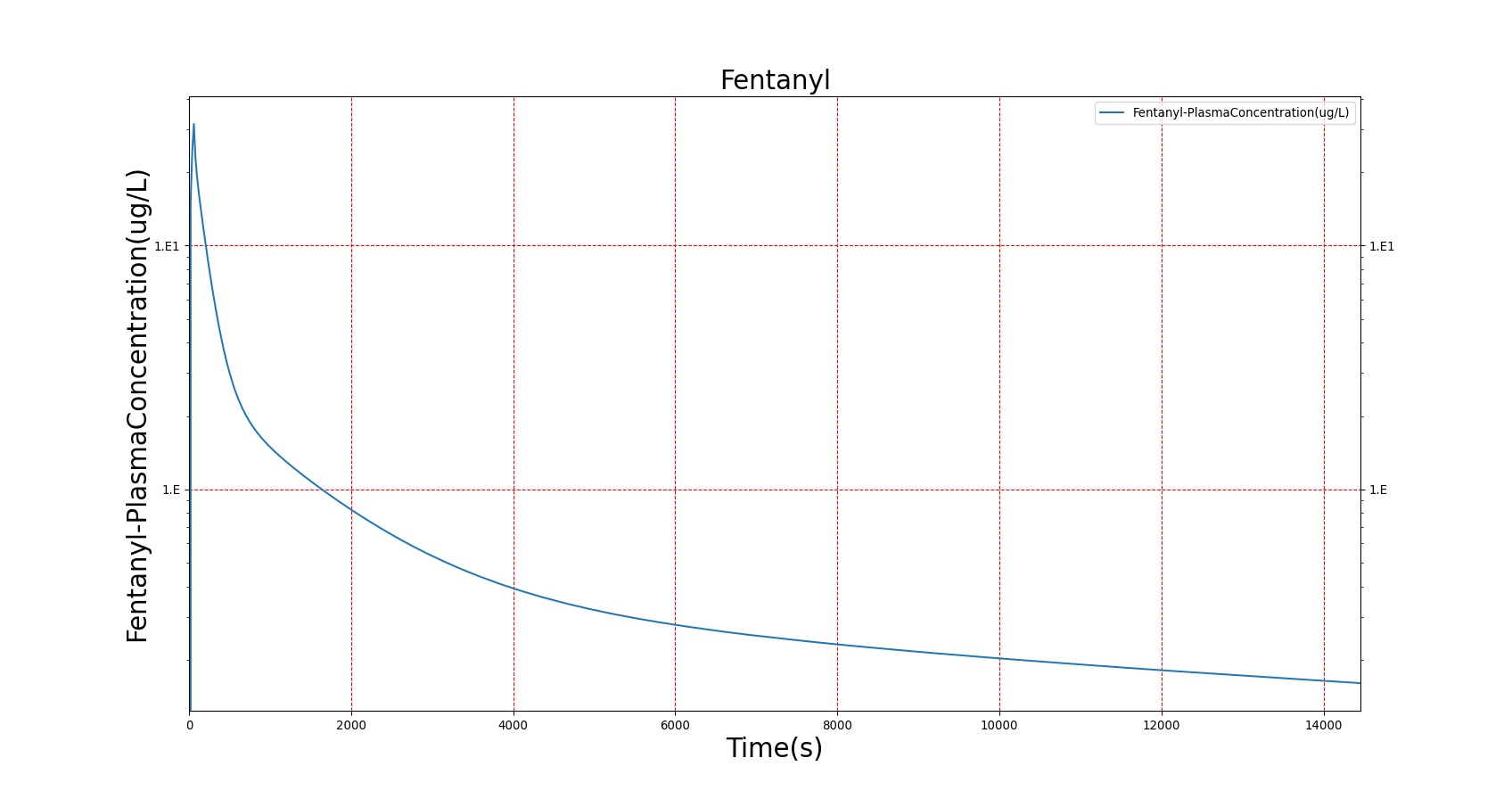
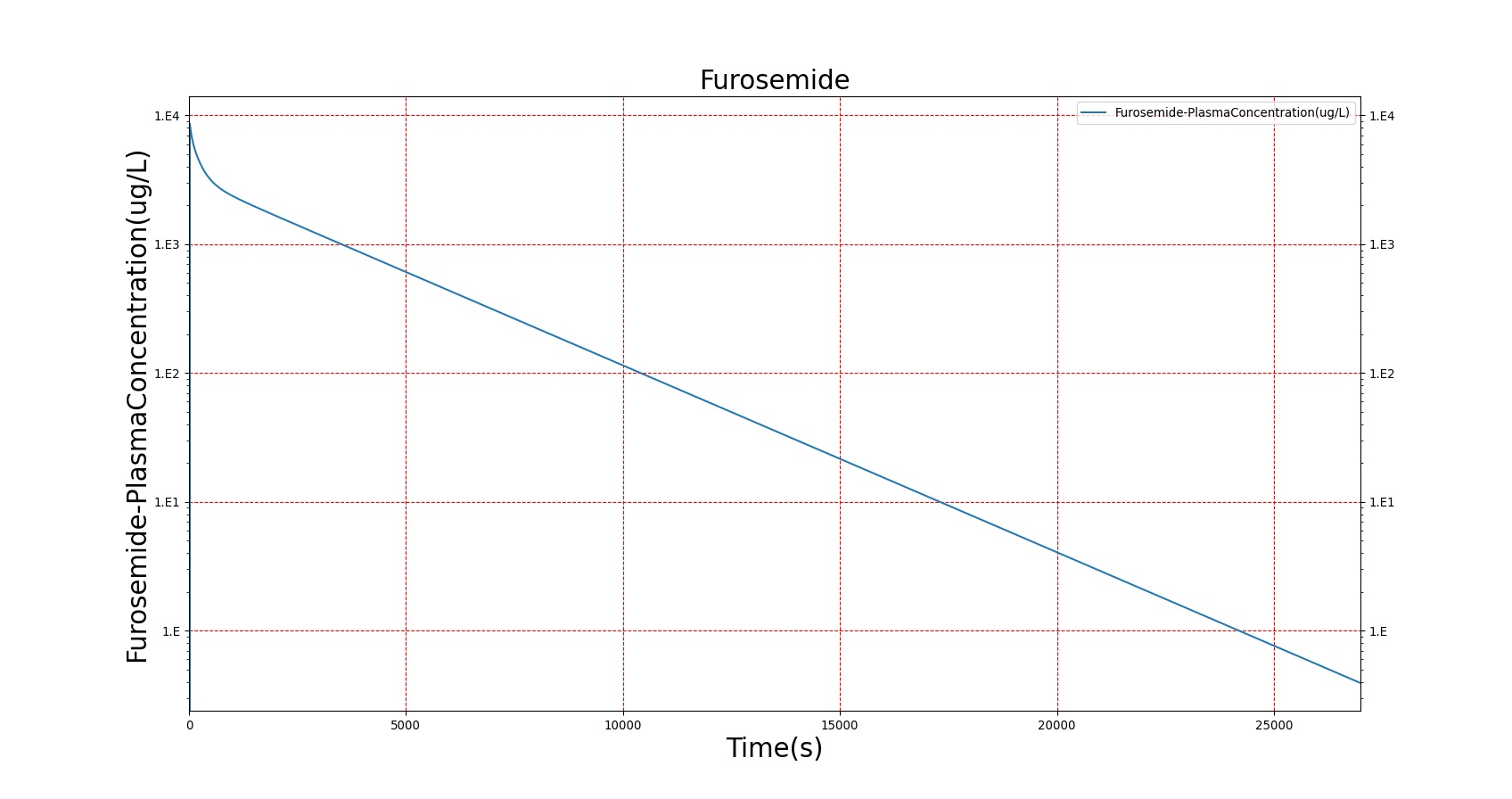
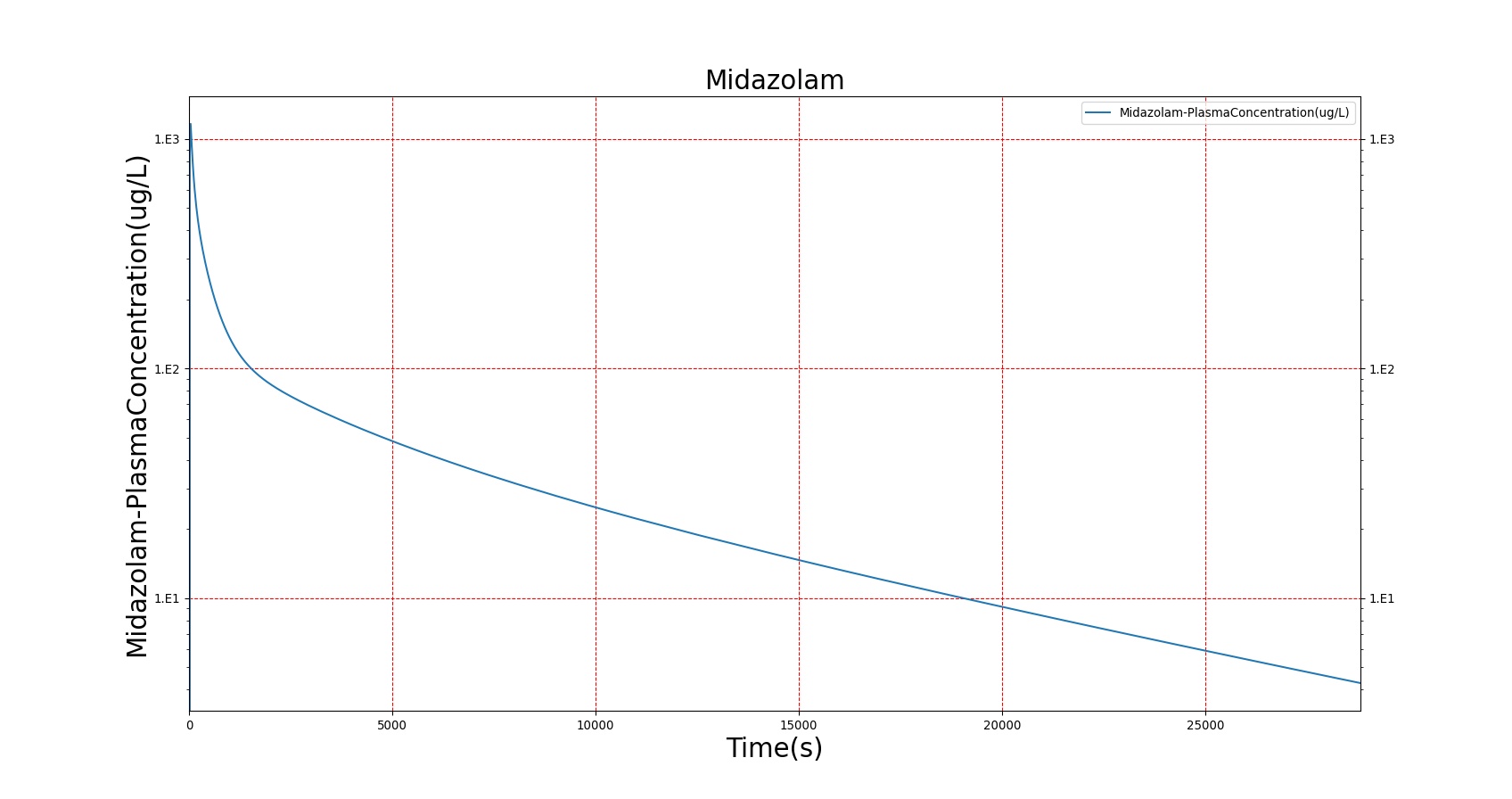
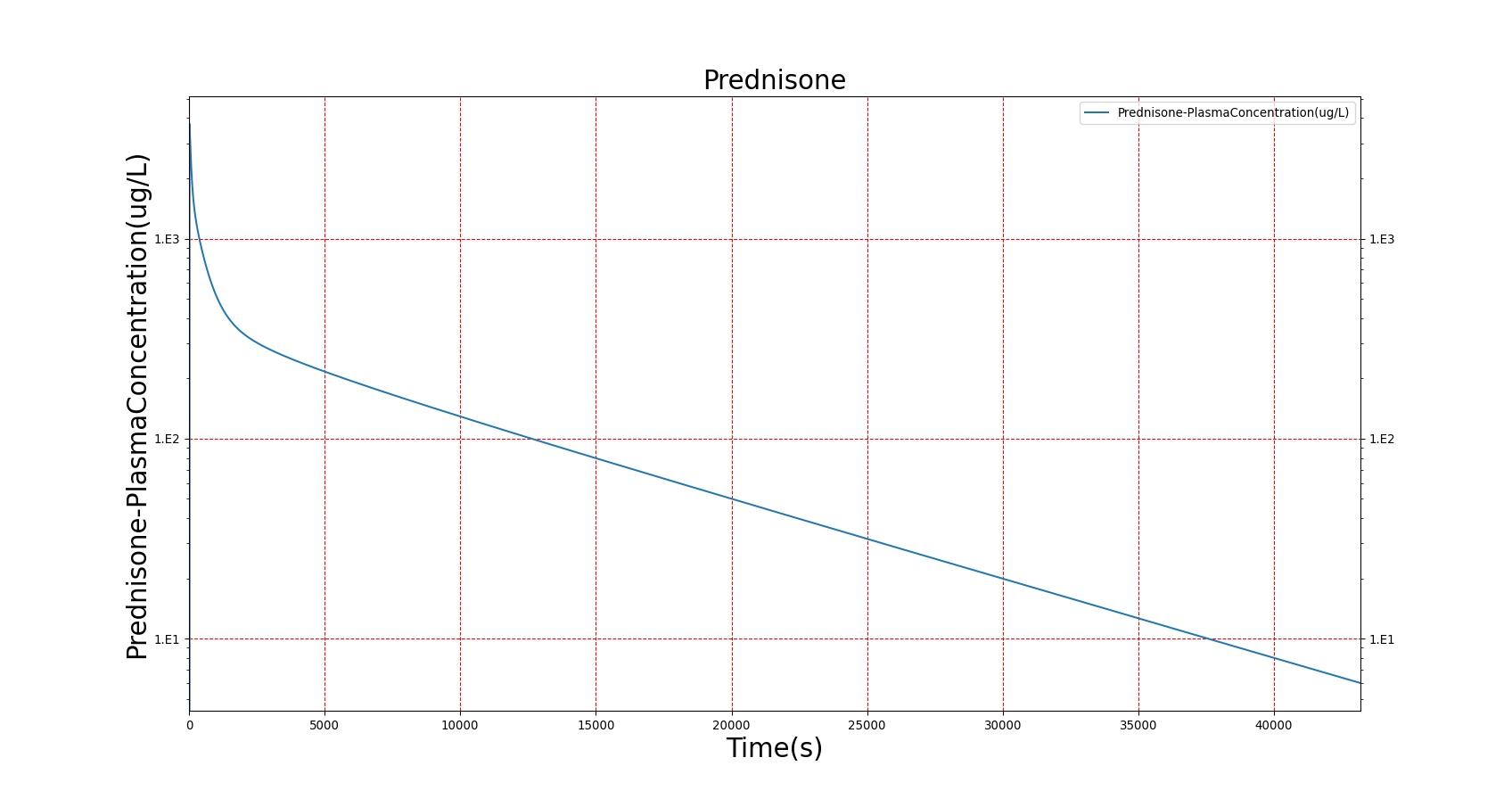
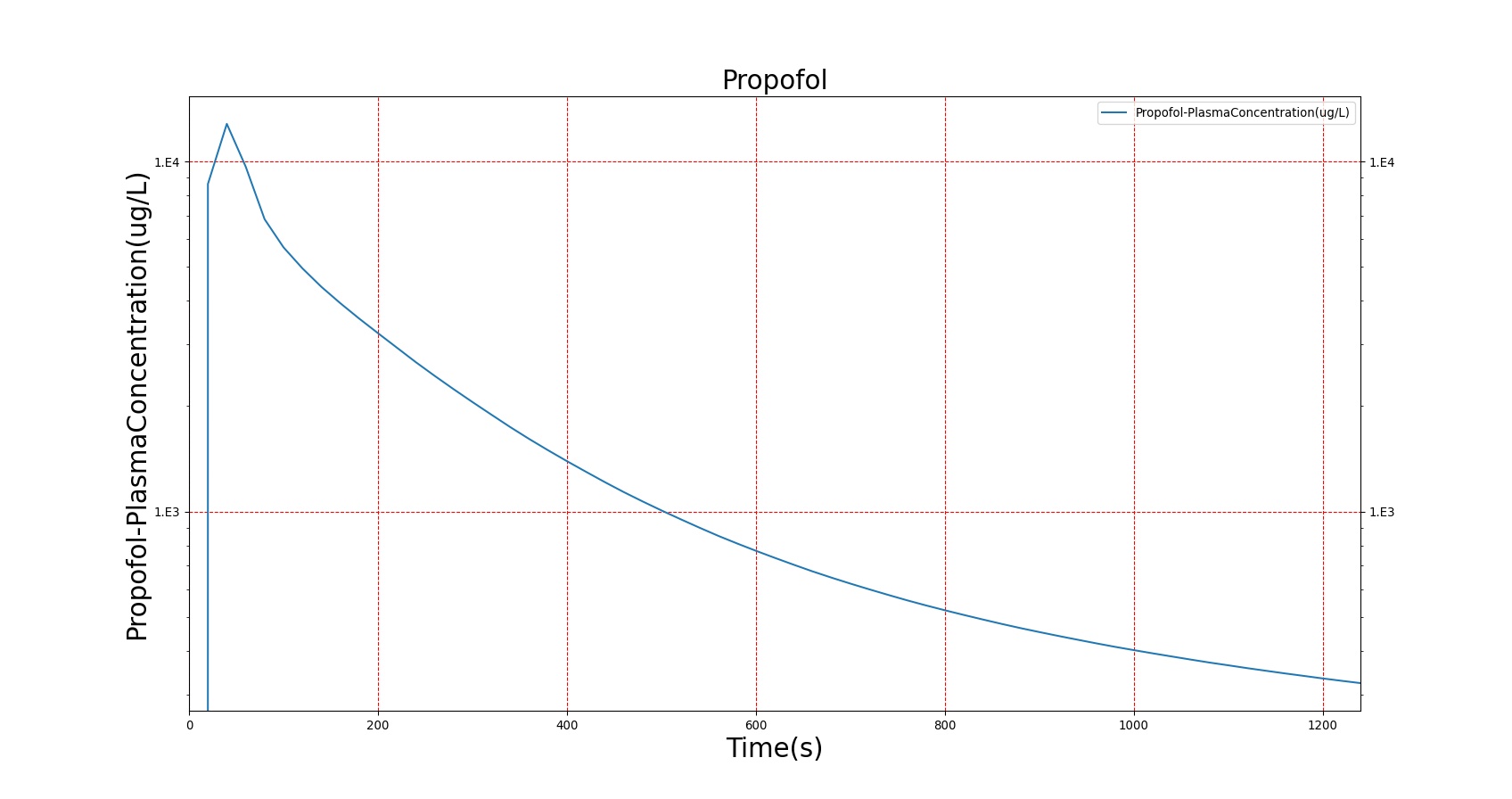
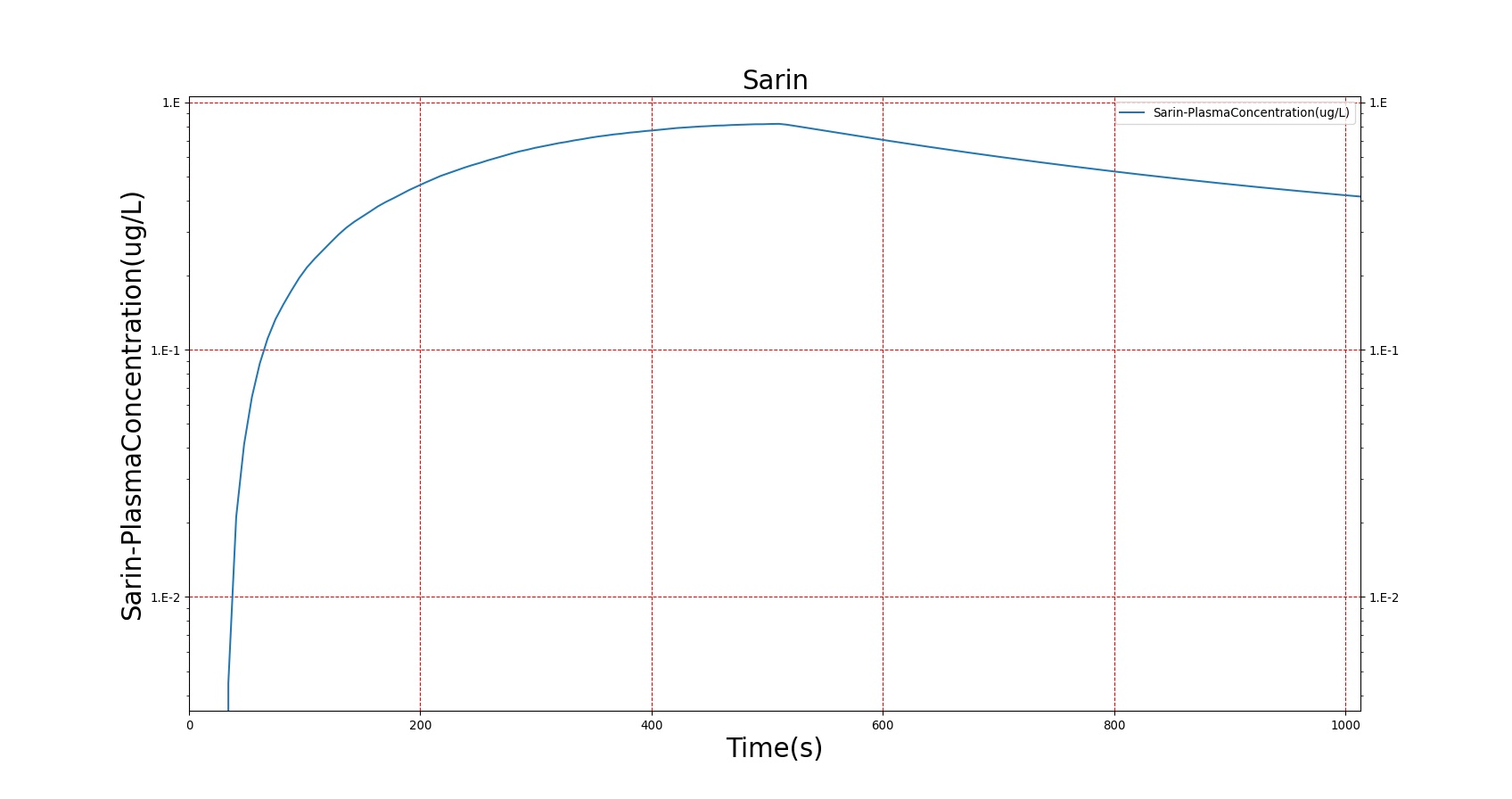
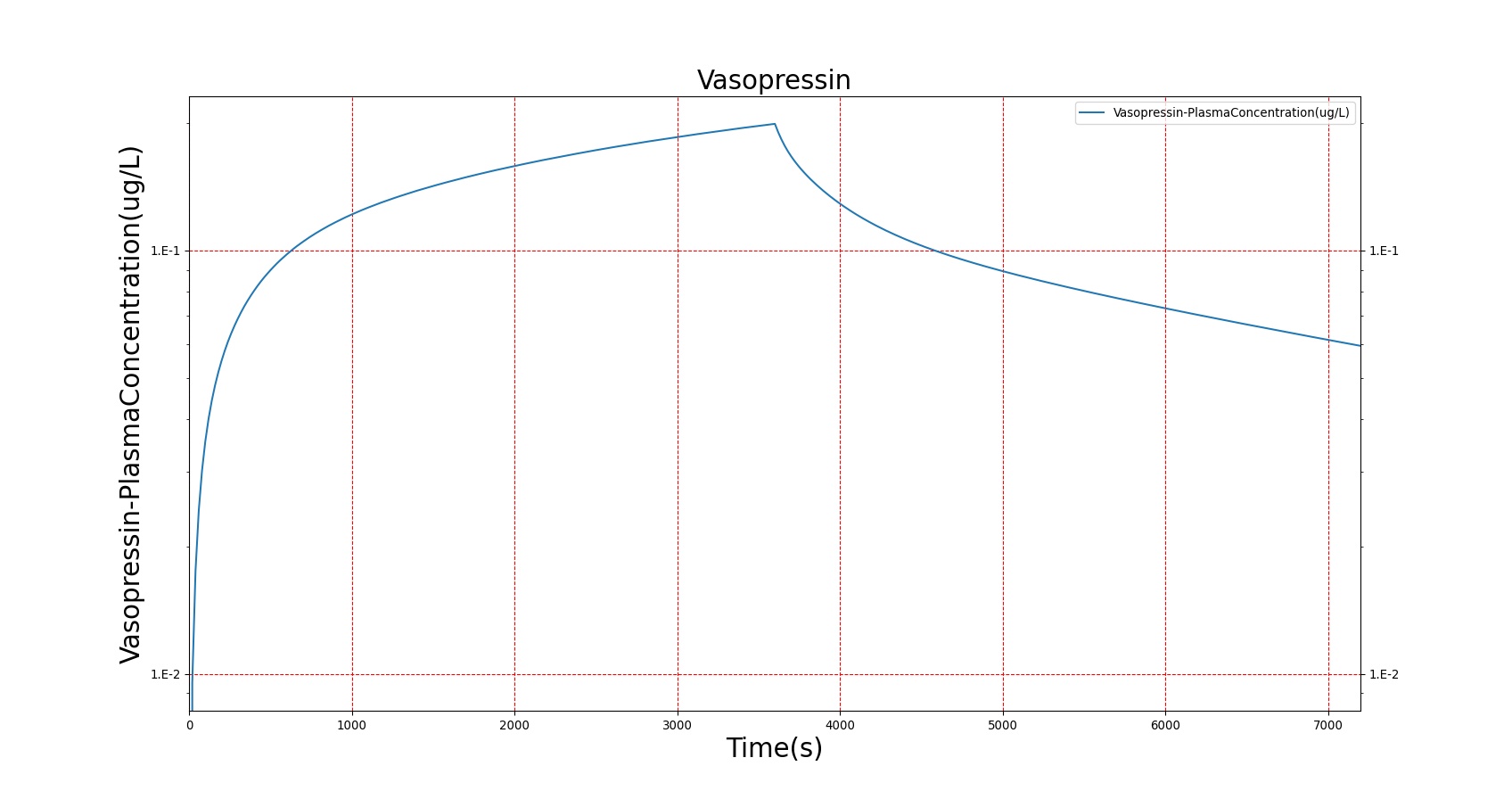
The above results show that, in general, the model chosen for BioGears produces good agreement between experimental and calculated data. However, it also reveals that for some drugs, this model does not appear to be valid. Future work will investigate the incorporation of vaporized substance methodologies, and additional partition coefficient calculations that may prove more accurate for specific drug types. Further statistical analysis will also be undertaken to assess the model performance rather than solely relying on a qualitative analysis.

Validation - Pharmacodynamic

The pharmacodynamic effects of the drugs were validated by comparing the effects of each drug to a number of clinical parameters. A summary of the drug validation is shown in Table 5. More details on the individual scenario validation can be found in the Drugs Scenario Validation Matrix.

Table 5. The BioGears drug library was validated qualitatively with published values and using subject matter expertise. Green indicates good agreement with validation data, yellow indicates agreement with a general trend with some minor disagreement, and red indicates a disagreement with the validation data. The number indicates the number of output parameters for each category of validation success or failure.

Scenario	Description	Good	Decent	Bad
Albuterol	Administer 90 ug metered dose of Albuterol	5	0	0
Desflurane	6% Desflurane breathed in through mask	4	2	0
Epinephrine	Adminster 10 ug injection of Epinephrine	4	1	0
Fentanyl	Administer 17 mg injection of Fentanyl	5	0	0
Furosemide	Administer 40 mg of Furosemide	3	1	0
Ketamine	Administer 115 mg injection of Ketamine	4	1	0
Midazolam	Administer 5 mg injection of Midazolam	5	0	0
Morphine	Administer 2.75 mg/min IV Morphine for 4 minutes	5	0	0
Morphine Overdose	Administer 8.2 mg/min IV Morphine for 24 minutes	3	2	0
Naloxone	Administer 17 mg injection of Fentanyl Followed by 30 ug injection of Naloxone *Validating only Naloxone	5	0	0
Pralidoxime	Adminster 700 mg injection of Pralidoxime	5	0	0
Prednisone	Administer 20 mg injection of Prednisone	5	0	0
Propofol	Administer 135 mg injection of Propofol	4	0	0
Rocuronium	Administer 52 mg injection of Rocuronium	2	0	0
Sarin	Exposure to 5 concentrations in the environment	21	4	0
Succinylcholine	Administer 96 mg injection of Succinylcholine	3	2	0
Tranexamic Acid	Administer 200 mg of TXA	8	0	0
Vasopressin	Ramp dose of vasopressin from 0.04 to 0.18 to 0.25 ug	3	2	0
	Total	94	15	0

Table 6. The validation results for liquid-modeled drugs.

Event	Notes	Action Occurrence Time (s)	Sample Scenario Time (s)	Heart Rate (beats/min)	Systolic Pressure (mmHg)	Diastolic Pressure (mmHg)	Respiration Rate (breaths/min)	Oxygen Saturation
Administer Epinephrine - 10ug	Drug Onset < 1 minute	30	30	25-50% Increase [242]	25-50% Increase [242]	25-50% Increase [242]	NC [242]	NC
Administer Fentanyl - 300 ug	Drug Onset 2-4 minutes	30	600	Stable [113] p192-7, [257] p277; 5-10% Decrease [242]	Stable [113] p192-7, [257] p277; 5-10% Decrease [242]	Stable [113] p192-7, [257] p277; 5-10% Decrease [242]	Decrease ˜ 50% [221], [407]	Decrease below 95% [221]
Administer Ketamine - 115 mg	Drug Onset < 1 minute	30	300	Moderate Increase [113] p200; 15-25% Increase [242]	Moderate Increase [113] p200; 15-25% Increase [242]	Moderate Increase [113] p200; 15-25% Increase [242]	Mild Decrease [113] p200; 25-50% Decrease [242]	NC
Administer Midazolam - 5 mg	Drug Onset in 1-3 min and lasts 30-60 minutes	30	70	Mild Increase [113] p200; 5-10% Decrease [242]	Moderate Decrease [113] p200; 15-25% Decrease [242]	Moderate Decrease [113] p200; 15-25% Decrease [242]	Moderate Decrease [113] p200; Marked Decrease To 0 [242]	As long as some respiration rate, little change. If RR=0, then begins to drop along O2 curve.
Administer Morphine - 2.75 mg/min	Constant rate of infusion for 4 minutes (11 mg total)	30-270	5000	Decrease 4-10% [349]	Minimal Decrease [349] or NC [122]	Minimal Decrease [349] or NC [122]	Decrease 25-30% [247]	Remain above 95% [317]
Administer Naloxone - 200 ug - in response to Fentanyl	Naloxone is modeled as a competitive inhibitor of opioids; it exhibits minimal PD effects alone	30 = 300 ug Fentanyl; 300 = 200 ug Naloxone	250; 1000	Return to resting state [122]	Return to resting state [122]	Return to resting state [122]	Return to resting baseline [122]	Increase
Administer Prednisone - 20 mg	Drug Onset in less than 1 minute	30	100	NC [306]	NC [306]	NC [306]	NC [306]	NC [306]
Administer Propofol - 200 mg	Drug Onset in less than 1 minute	30	70	NC [113] p200; NC [242]	Marked Decrease [113] p200; 25-40% Decrease [242]	Marked Decrease [113] p200; 25-40% Decrease [242]	Marked Decrease [113] p200; 100% Decrease [242]	Begins to drop according to O2 curve
Administer Rocuronium - 50 mg	Drug Onset in 60-90 seconds	30	100	NC [257] p299; NC [242]	NC [257] p299; NC [242]	NC [257] p299; NC [242]	Goes to Zero [113] p224; Goes to Zero [242]	Begins to drop according to O2 curve
Administer Succinycholine - 77 mg	Drug Onset < 1 minute	30	70	Mild Increase [113] pp210-5; 5-10% Decrease [242]	Mild Increase [113] pp210-5; 5-10% Decrease [242]	Mild Increase [113] pp210-5; 5-10% Decrease [242]	Goes to Zero [113] p224; Goes to Zero [242]	Begins to drop according to O2 curve
Administer Vasopressin – 0.04, 0.18, and 0.25 ug	Infusions are successive, each lasts 20 minutes	30, 1230, 2430	2430	Decrease ˜ 25% [224]	Increase 7-8 mmHg [224]	Increase 7-8 mmHg [224]	NC [224]	NC [224]

Table 7. The validation results for gas-modeled drugs.

Event	Notes	Action Occurrence Time (s)	Sample Scenario Time (s)	Heart Rate (beats/min)	Systolic Pressure (mmHg)	Diastolic Pressure (mmHg)	Respiration Rate (breaths/min)	Tidal Volume (mL)	Oxygen Saturation
Administer Albuterol - 10ug	Drug Onset < 1 minute	30	200	25-50% Increase [131]	Slight Increase [131]	Slight Increase [131]	NC [131]	NC [131]	NC

Table 8. The validation results for furosemide.

Event	Notes	Action Occurrence Time (s)	Sample Scenario Time (min)	Urine Production Rate (mL/min)	Chloride Excretion (mmol/min)	Sodium Excretion (mol/min)	Vascular Volume (mL)
Administer Furosemide - 40 mg	Drug Onset < 1 minute	30	450	300-400% Increase [175]	300-400% Increase [175]	300-400% Increase [175]	Decrease (around 500-1000 mL) [139]

Diuretic-Furosemide

PD effects for the diuretic Furosemide are handled differently than other drugs in the BioGears patient. Localized effects are implemented via a tubular permeability modifier. This effectively simulates Furosemide's effect on the tubular luminal Na-K-Cl co-transporter, inhibiting reabsorption of fluid and ions into the vasculature, as shown in Figure 19. The permeability modifier is a function of drug concentration in the blood plasma. These concentrations determine appropriate tubular reabsorption inhibition by reducing the permeability of the tubular lumen (for more information, see Renal Methodology). This effectively increases the urine production rate and ion excretion, and reduces the patient's total blood volume. To see the effects of the drug on the cardiovascular system during ventricular systolic dysfunction, see Cardiovascular System.

Figure 19. The diuretic furosemide causes an inhibition of reabsorption due to its effect on the tubular lumen co-transporter. Total blood volume decreases as urine production and ion excretion increase. Eventually, as the body clears the drug, urine production and ion excretion both begin to return to normal.

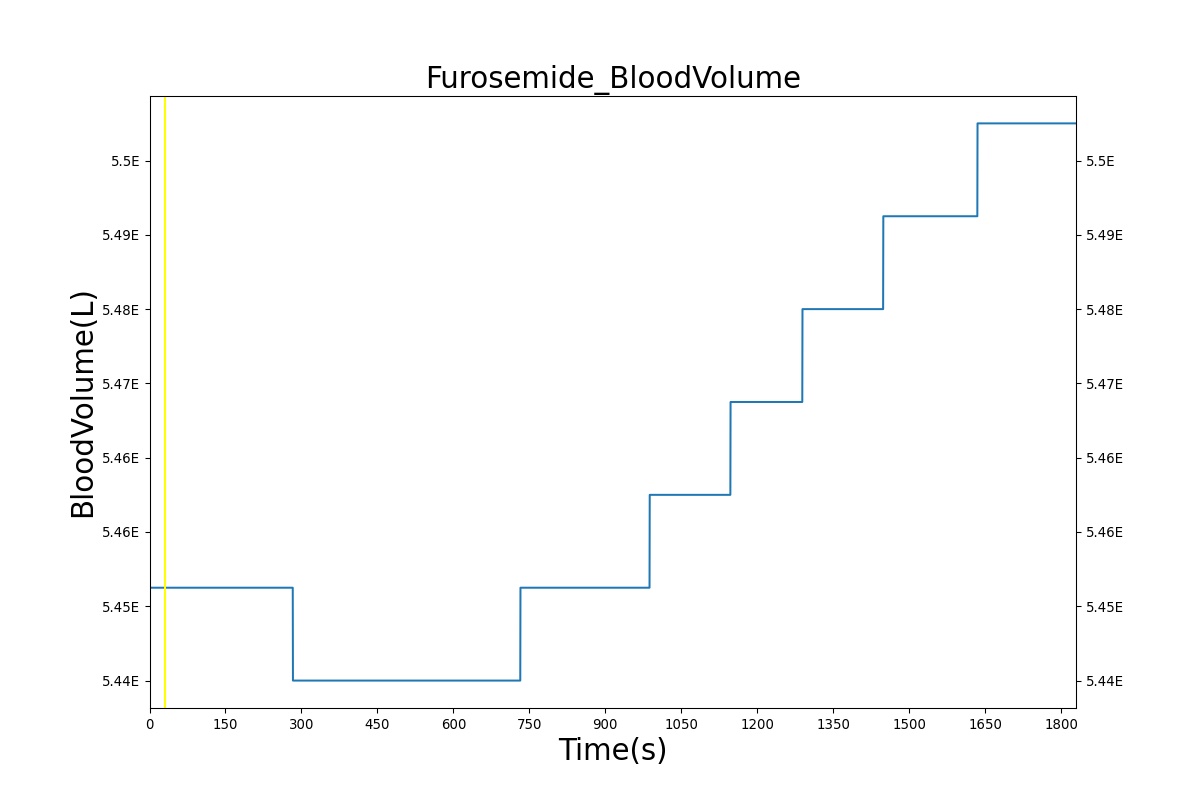
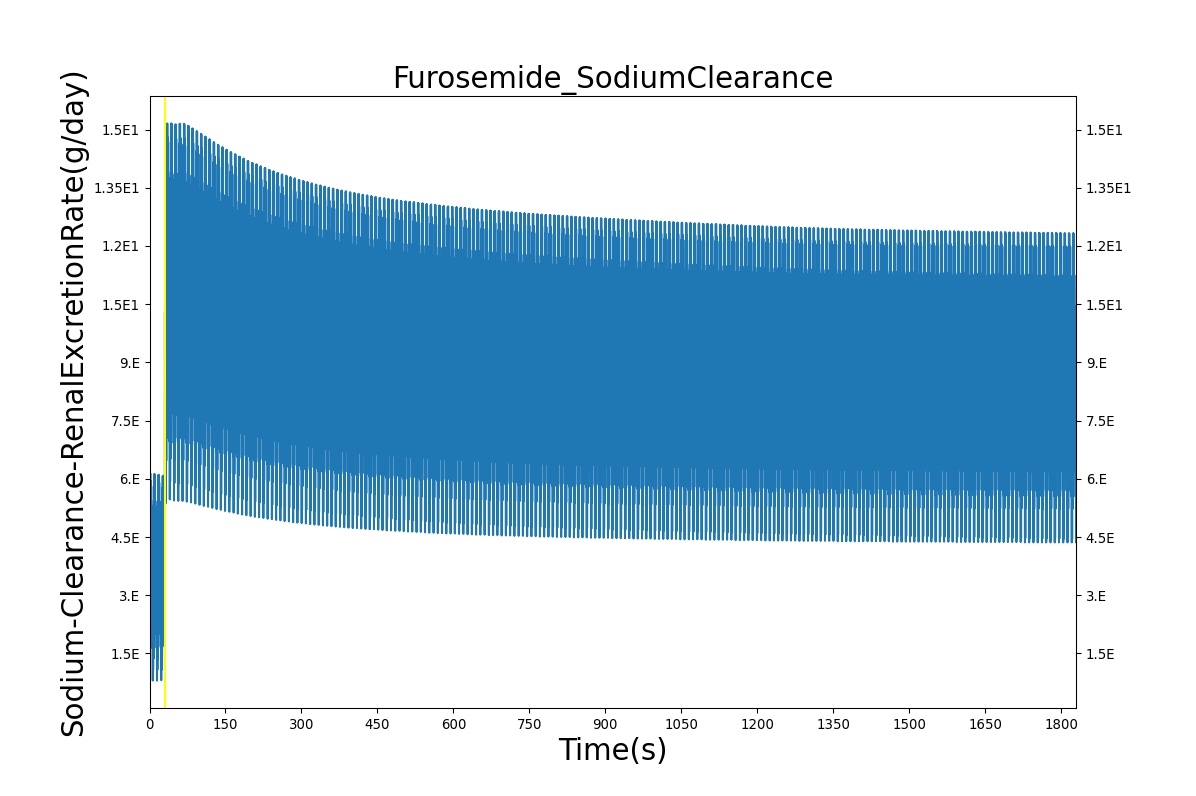
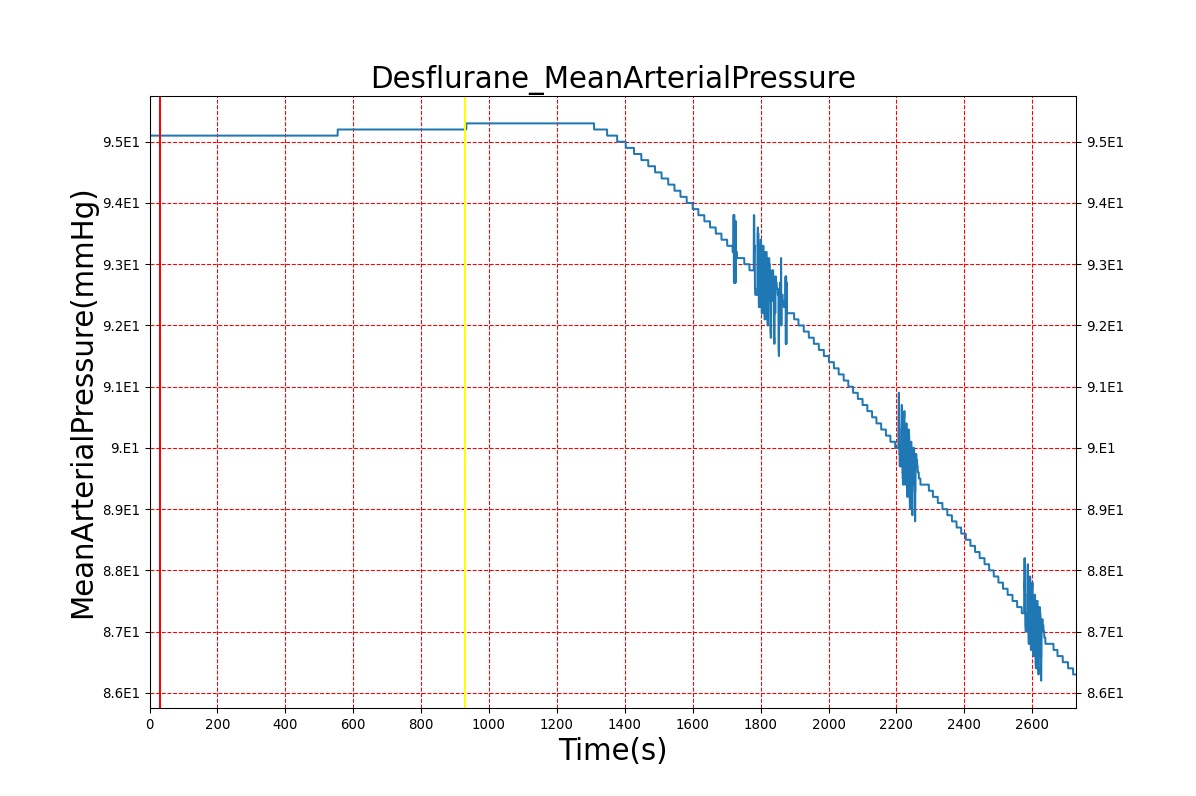
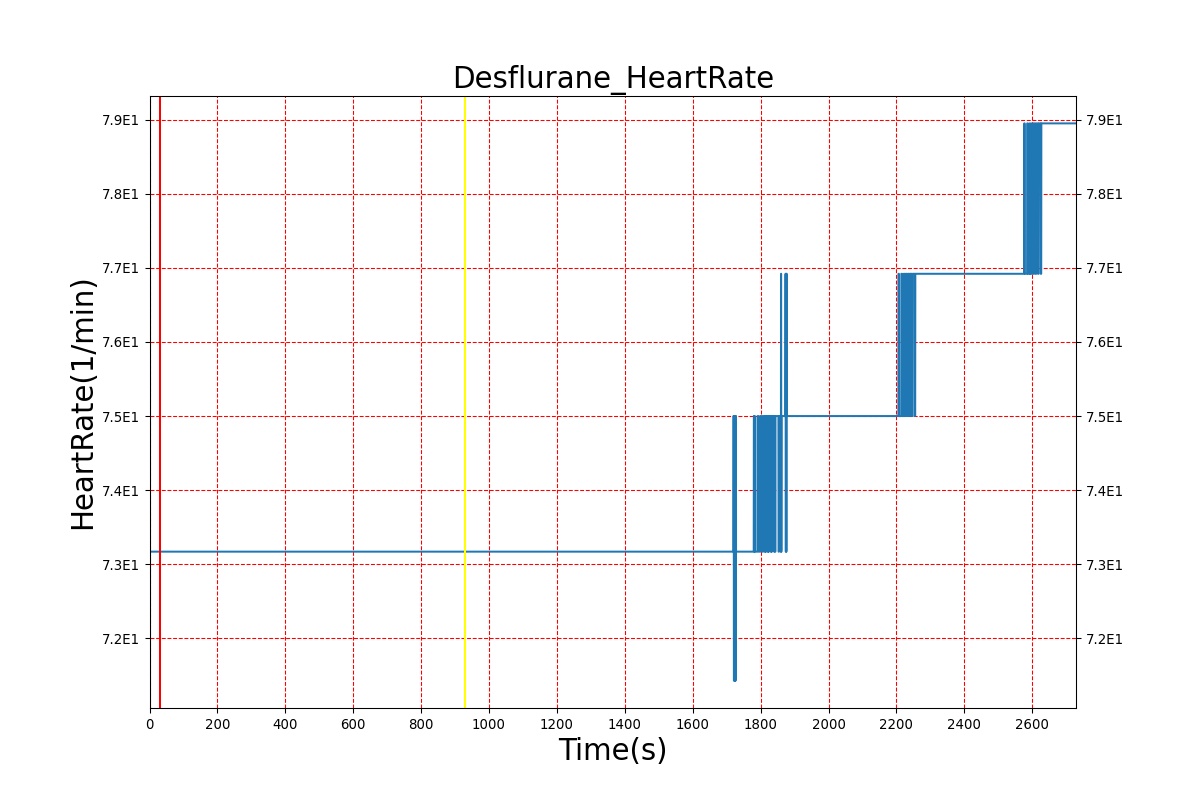
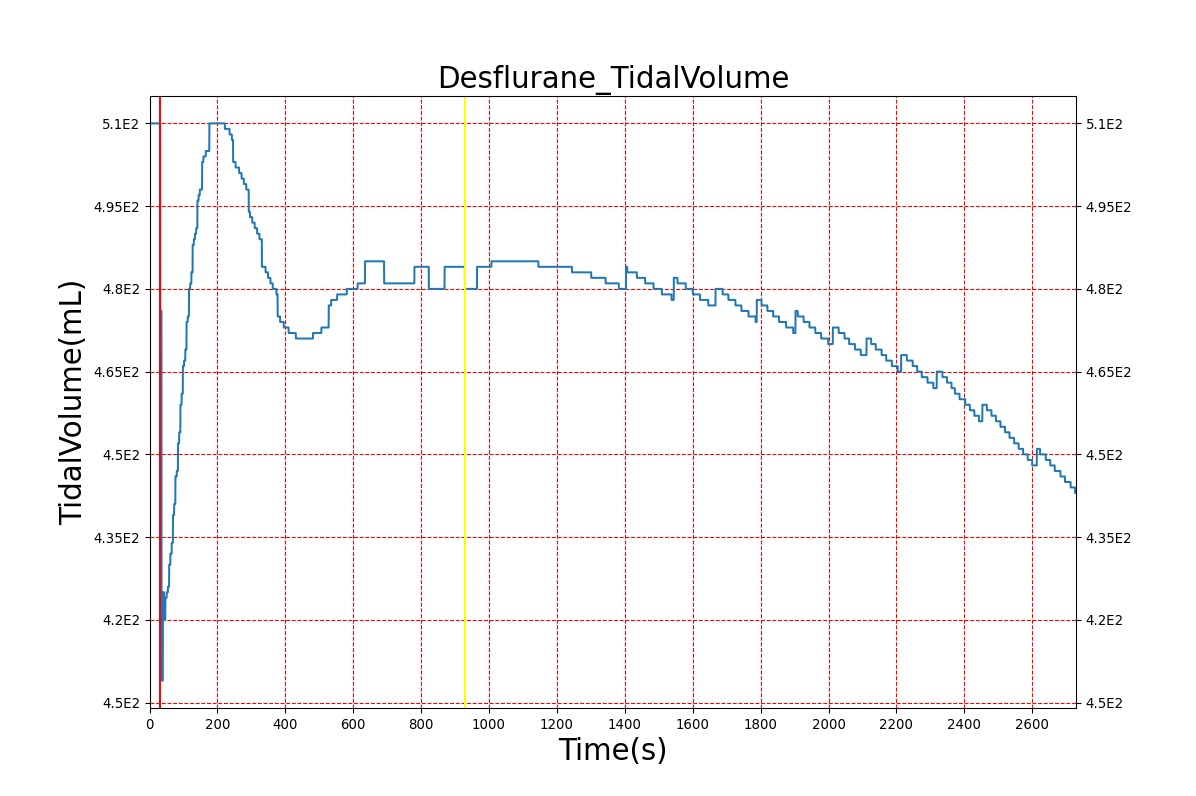
Volatile Anesthetic-Desflurane

Table 9. Data was obtained from studies in which healthy volunteers breathed desflurane spontaneously without any other anesthetic agent (i.e. nitrous oxide, propofol, etc.) [385] [188].

Event	Notes	Action Occurrence Time (s)	Sample Scenario Time (s)	Heart Rate (beats/min)	Mean Arterial Pressure (mmHg)	Systemic Vascular Resistance (mmHg-s/mL)	Cardiac Output (L/min)	Respiration Rate (breaths/min)	Tidal Volume (mL)
Administer-Desflurane 6%	Drug Onset < 1 minute	80	1000	Approx. 20% increase [385] p169	Approx. 34% decrease [385] p169	Approx. 54% decrease [385] p169	Approx. 30% increase [385] p168	Approx. 60% increase [188] p485	Approx. 35% decrease [188] p485

Figure 20. The anesthetic desflurane suppresses mean arterial blood pressure by decreasing systemic vascular resistance. Heart rate increases and, in the case of spontaneously breathing patients [385], so too does cardiac output (though not to the degree predicted). Desflurane also impacts the respiratory system by increasing respiration rate and decreasing tidal volume.

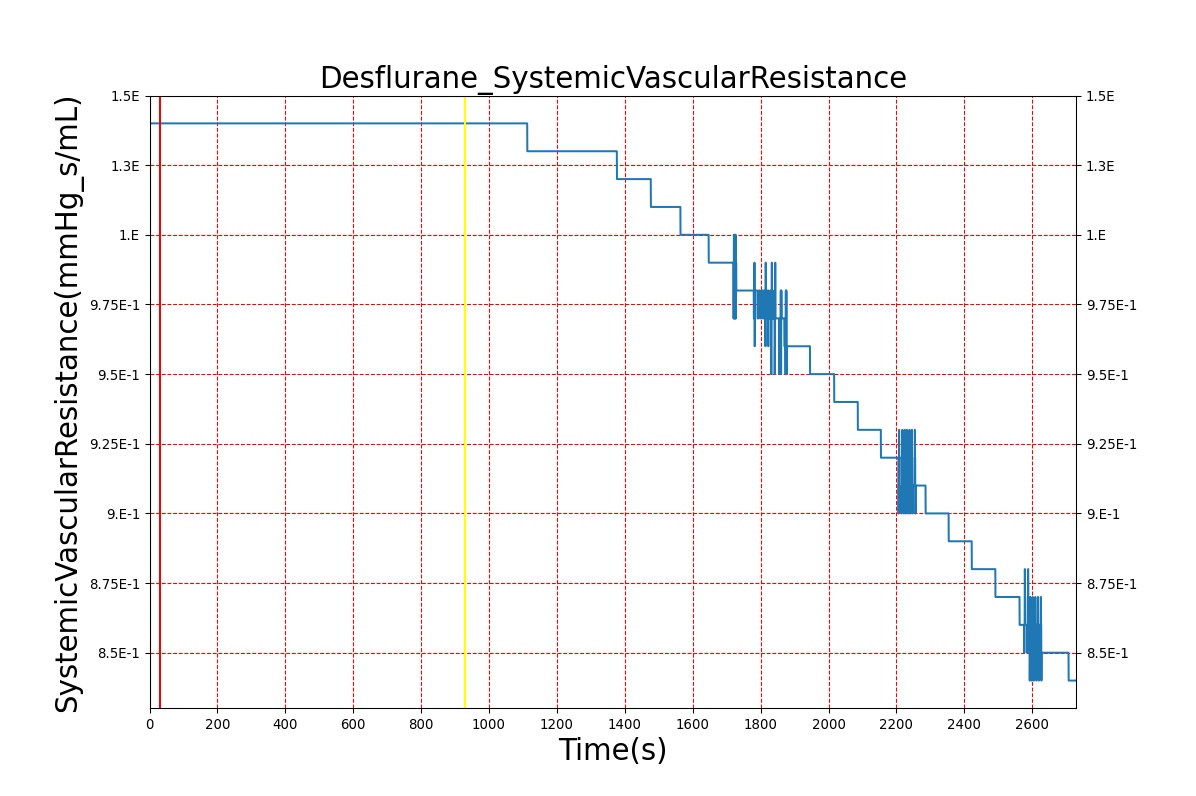
Advanced Models

As we work to continuously improve the BioGears Drugs System, we have introduced models that incorporate more advanced features such as Overdose, Drug-Drug Interactions, and Target/Receptor Occupancy. These new capabilities are currently available with respect to the opioids morphine and fentanyl and to the nerve agent Sarin. We plan to generalize these advanced components to the remaining drugs in our library with the goal of increasing overall model accuracy while maintaining flexibility.

Opioids

Morphine Intoxication

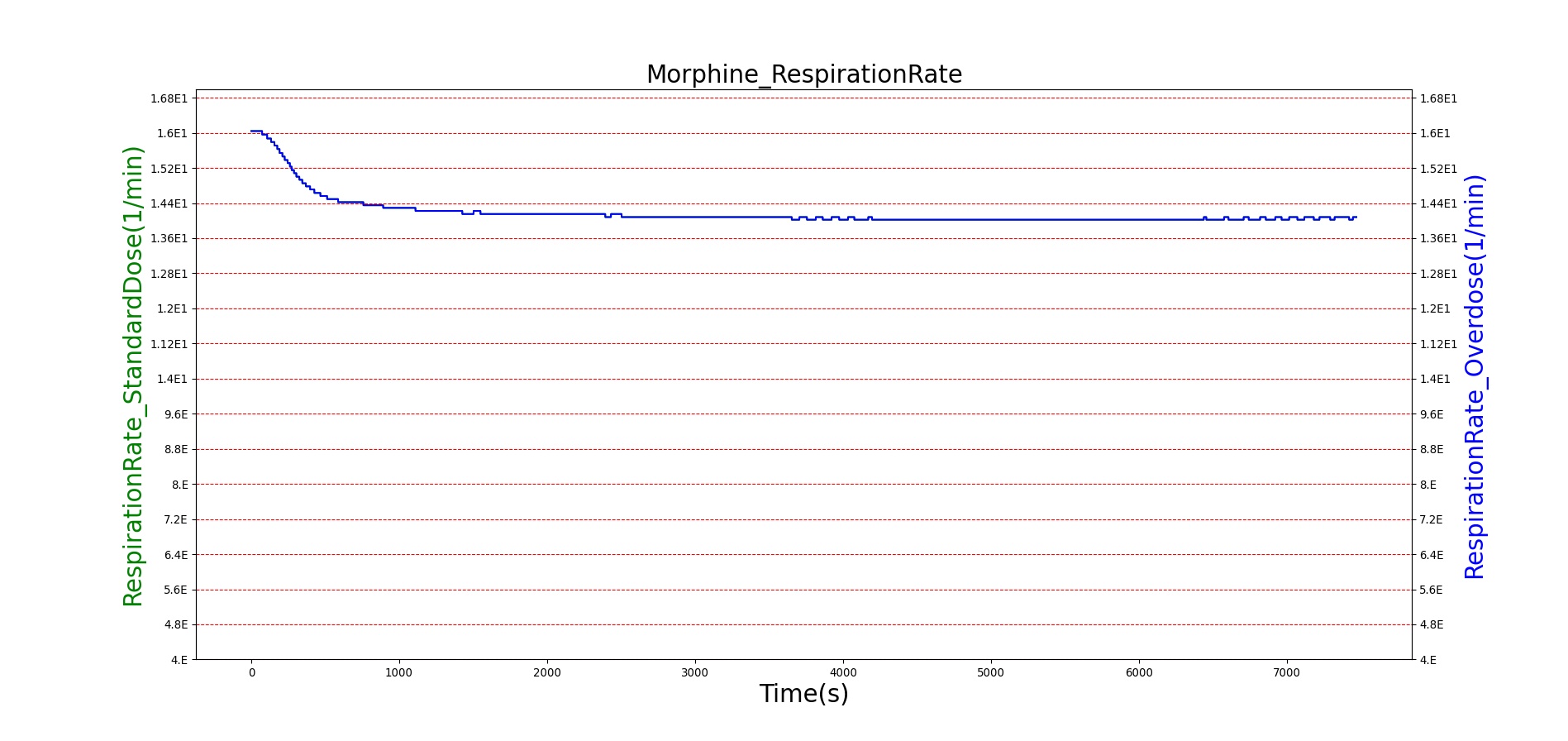
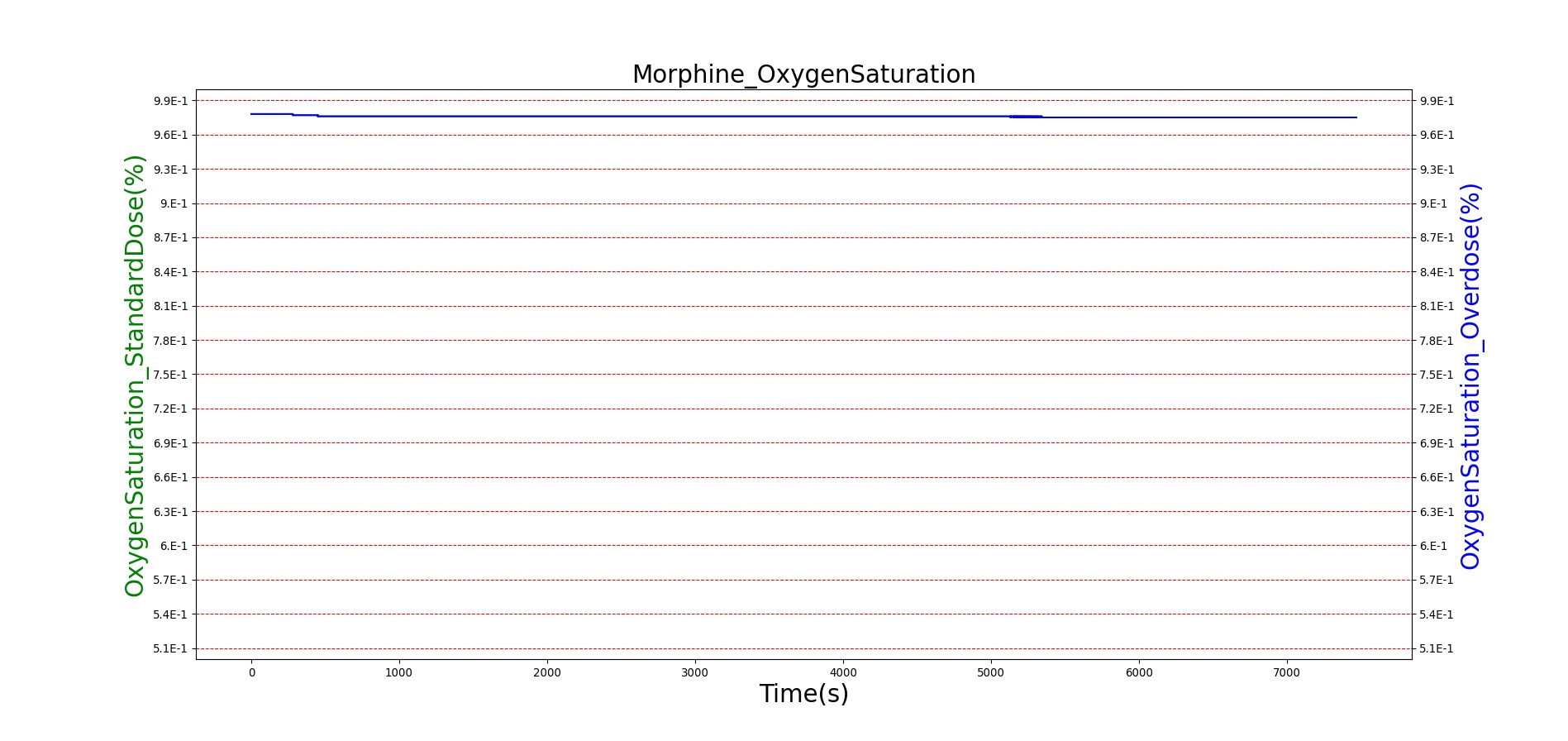
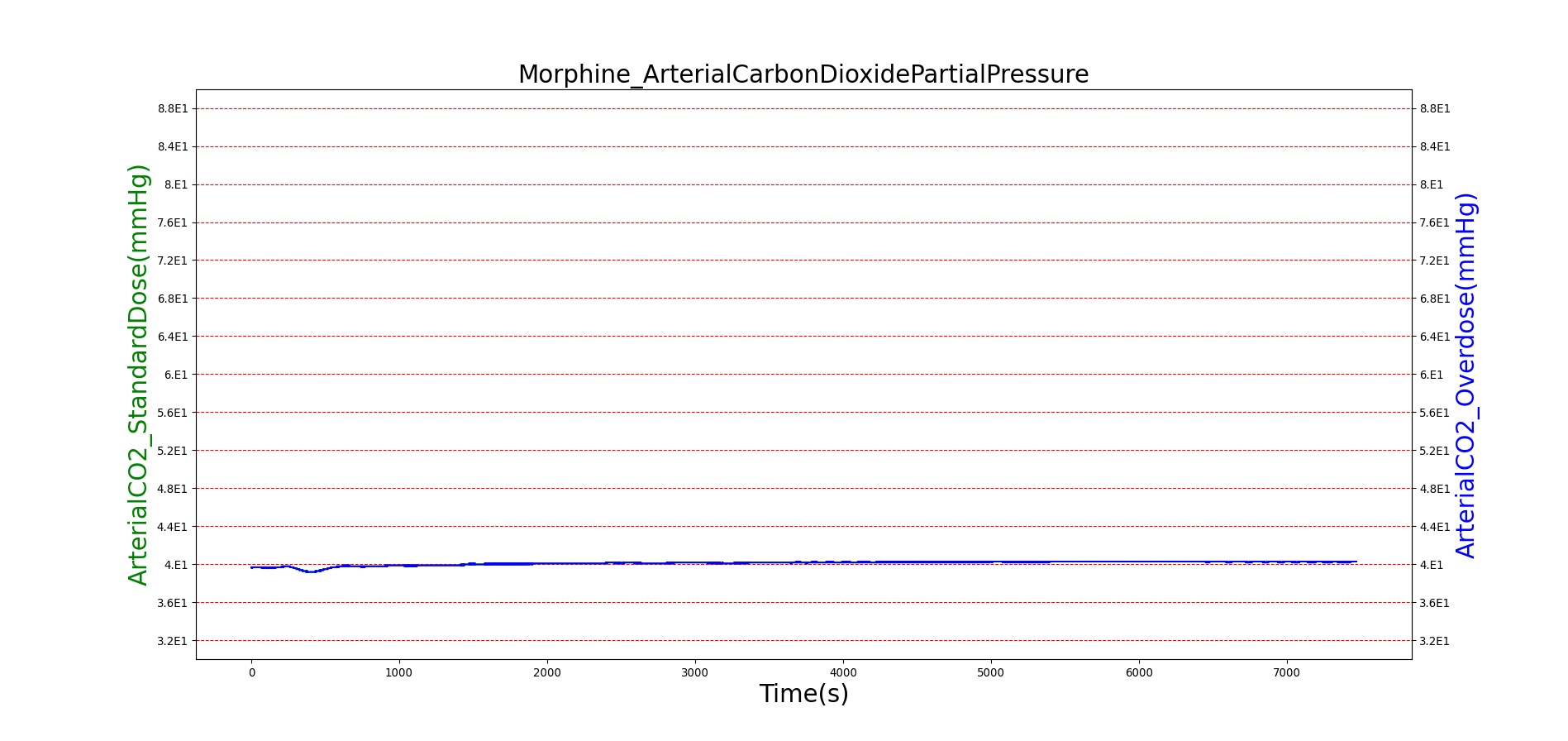
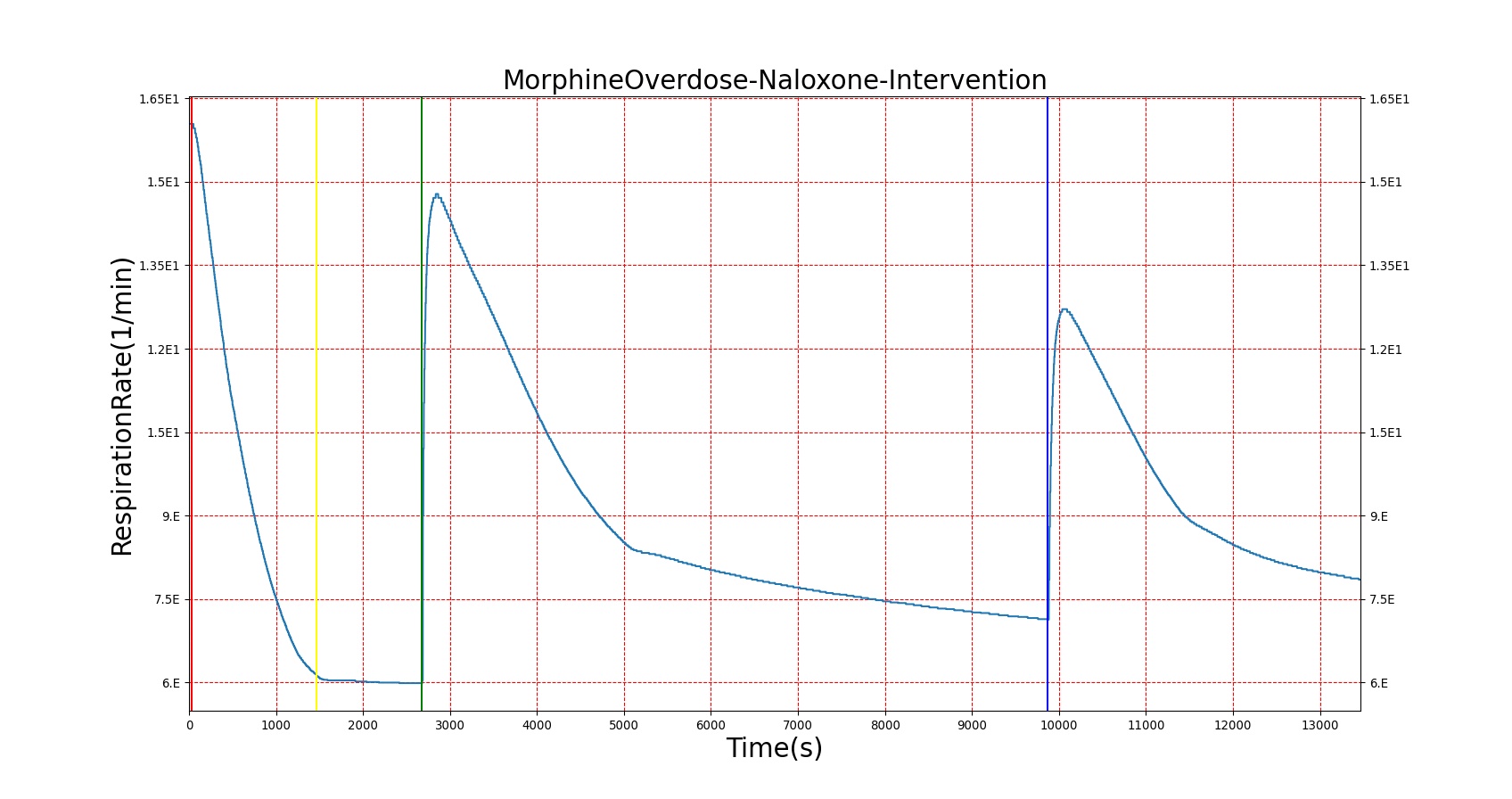
Morphine is the first drug in the BioGears library with parameters tuned to model overdose scenarios. The BioGears overdose scenario is modeled after a case report in which a patient received 200 mg of intravenous Morphine over 24 minutes from a defective patient controlled analgesic (PCA) device and experienced severe opioid ventilatory impairment (OIVI) [77]. Morphine PD parameters were tuned to produce symptoms consistent with OIVI (respiratory depression, hypercapnia, and hypoxia) using both this report and other supporting literature (see Table 10). Figure 21 compares the severe overdose scenario to the standard Morphine dose. Note the prolonged nature of the pharmacological effects, which is a function of Morphine's low effect site rate constant (k_e = 0.0026 1/min). In this scenario, the patient does not enter an irreversible state (though one will be triggered at higher doses), making our model somewhat conservative. We took such a conservative approach because opioid sensitivity is extremely variable among patients, particularly between men and women [253]. It should also be mentioned that the tidal volume predicted by our model (not shown) erroneously demonstrates a substantial increase. This is a known issue resulting from the manner in which tidal volume and respiration rate are coupled in the current BioGears respiratory system (see Respiratory Methodology) and will be an area of future work.

Table 10. Comparison of the BioGears response to a standard dose of Morphine ([349]) and an overdose of Morphine ([77]). The overdose produces symptoms consistent with opioid induced ventilatory impairment (OIVI) and bradycardia.

Event	Notes	Action Occurrence Time (s)	Sample Scenario Time (s)	Respiration Rate (breaths/min)	Arterial Carbon Dioxide Pressure (mmHg)	Oxygen Saturation (%)	Heart Rate (bpm)	Blood Pressure (mmg)
Administer Morphine-2.75 mg/min	Infused at constant rate over 4 minutes (11 mg total)	30-270	5000	Decrease 25-30% [247]	Increase < 4 mmHg [349]	Remain above 95% [317]	Decrease 4-10% [349]	Minimal Decrease [349] or NC [122]
Administer Morphine-8.2 mg/min	Infused at constant rate over 24 minutes (~197 mg total)	30-1470	7200	<=6 [122], [176]	>55 mmHg [197]	<85% for six minutes [57]	<60 [240]	Hypotension (SBP < 90 and DBP < 60) [240]

Figure 21. The Morphine overdose scenario shows the difference in effect betweeen a standard dose (red) an overdose (blue). The timeline below the plots shows the collection of respiratory events thrown in BioGears such as respiratory distress, hypoxia, and hypercapnia.

Reversal of Opioid Induced Respiratory Depression

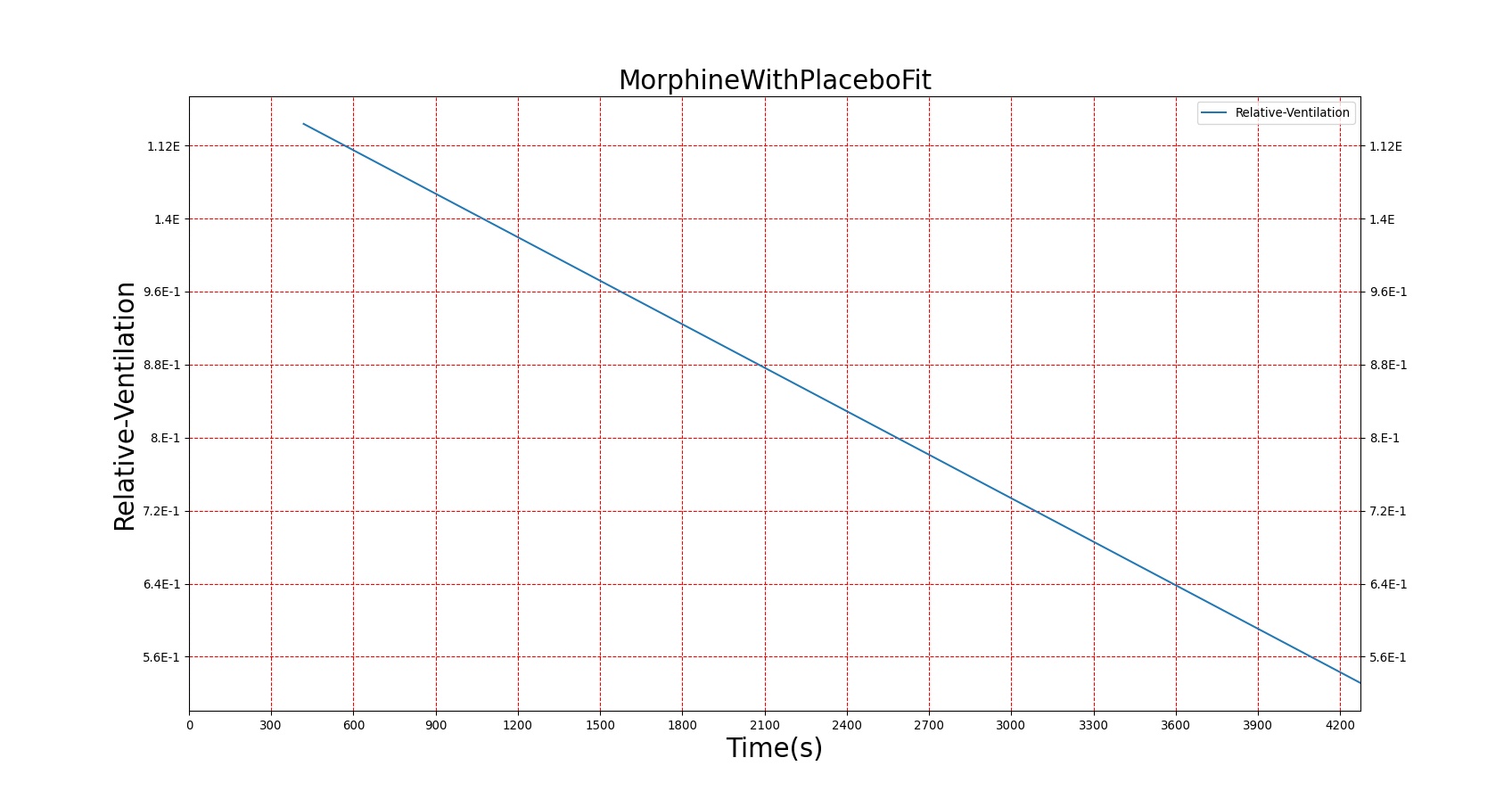
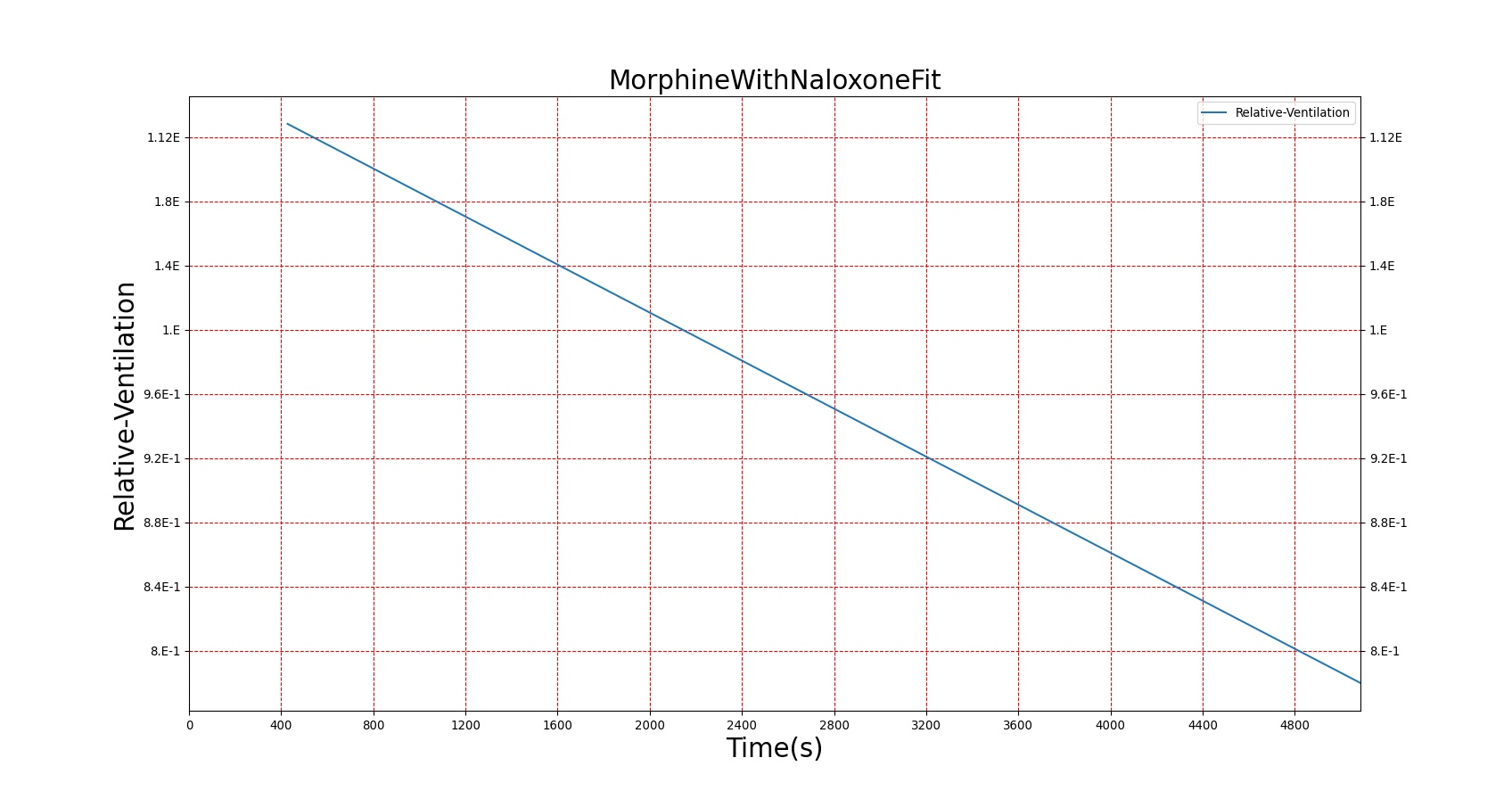
Severe respiratory depression resulting from opioid usage is commonly treated with naloxone. Naloxone competes with opioids at mu receptors in the central nervous system and, when bound, exerts essentially no pharmacodynamic effects [122]. Thus, as more opioids are displaced, symptoms progressively improve. This competitive interaction can be modeled using Equation 10. The inhibition constant (K_I) for Naloxone was estimated in two stages (see Figure 22) from data published in [247] regarding the combined effects of Morphine and Naloxone on respiration. First, the EC₅₀ for Morphine was estimated from human volunteers who were administered Morphine followed by placebo. This experimental EC₅₀ was then used to fit Equation 10 to data collected from individuals who were given Morphine followed by Naloxone and determine the best value for K_I. Since the EC₅₀ for Morphine utilized by BioGears is not equivalent to the one determined from this study (this is due to the fact that BioGears is tuned for multiple pharmacodynamic responses and not just breathing rate), the ratio of the estimated EC₅₀ to K_I was used to determine the BioGears K_I. It was assumed that this K_I is appropriate for the interaction of Naloxone and Fentanyl, which seems appropriate given that Fentanyl acts predominantly on the same receptor as Morphine.

Figure 22. Non-linear least squares regression after estimation of Morphine EC₅₀ and Naloxone K_I. Experimental data was obtained from [247] in which patients were administered 0.15mg/kg intravenously followed by a placebo (left) or 400 ug of intravenous Naloxone (right).

Figures 23-24 demonstrate the effect of administering naloxone after respiratory depression induced by Fentanyl and Morphine. Note that while the effects of Fentanyl are completely reversed after a standard Naloxone dose (115 ug [247]), depression of respiratory activity persists in the case of morphine (renarcotization). In the case of massive overdose, the degree of renarcotization necessitates a second dose of naloxone. This result is due to the fact that Naloxone has a longer elimination half-life than Fentanyl but a significantly shorter one than Morphine (see Table 6 for Naloxone validation).

Figure 23. Naloxone reversal of respiratory depression induced by Fentanyl. Fentanyl protocol and pharmacodynamic parameters were obtained from [407]. Green = Infuse 300 ug of Fentanyl; Black = End of Infusion; Magenta = Administer 200 ug of IV naloxone.

Figure 24. Naloxone reversal of minor respiratory depression induced by standard dose of morphine (left) and major respiratory depression induced by morphine overdose (right). Left Figure: Green = Administer 10.5 mg bolus of intravenous morphine; Black = Adminster 200 ug of Naloxone. Right Figure: Green = Begin intravenous morphine infusion of 8 mg/min; Black = End of infusion; Magenta = Administer 800 ug of intravenous Naloxone; Yellow = Adminster 400 ug of intravenous Naloxone.

Nerve Gas: Sarin

The Chemical Weapons Convention (CWC) was initiated in 1993 to ban the synthesis of chemical warfare agents and outline a plan for the destruction of existing chemical stockpiles . Though certainly a positive development, chemical weapons, particularly nerve gases, remain of considerable interest due to their potential use as agents of terror. Perhaps the most well-known instance of chemical terrorism is the 1995 attack perpetrated by the extremist group Aum Shinrikyo on the Tokyo subway using the nerve agent Sarin [24]. That same compound, Sarin, has been more recently implicated in chemical attacks in Syria (a relatively new member to the CWC) in 2013 and 2017 [60]. We thus have selected Sarin as our model nerve agent.

Sarin belongs to a class of chemicals called organophosphates which exert their physiological effects by inhibiting the activity of the enzyme acetylcholinesterase. Acetylcholinesterase (AChE) catalyzes the breakdown of the neurotransmitter acetylcholine (ACh) in the peripheral and central nervous systems [26]. In the absence of AChE, ACh remains in high concentrations in synaptic junctions and continues to stimulate nerve signal transduction. Neural overstimulation leads to hyperactivity at receptors associated with muscle tissue, secretory glands, and the respiratory center (though seemingly disparate symptoms can occur as a result of ACh’s role in both the sympathetic and parasympathetic nervous responses) [122]. Prolonged exposure leads to death induced by central respiratory failure and paralysis of diaphragm muscles [26].

To compound matters, the bound Sarin-AChE complex does not spontaneously reverse; rather, it undergoes a subsequent reaction—called “aging”—which permanently deactivates AChE [67]. The aging process is the target of efforts to identify organophosphate-induced toxicity reversal agents. If the initial binding of Sarin to AChE can be reversed prior to aging, the functionality of the enzyme can be salvaged and the Sarin eliminated from the body. One class of compounds that has received close attention is the oximes, of which Pralidoxime (2-PAM) is the most frequently cited [194]. As Pralidoxime is also in the BioGears library, we easily incorporate it in our model.

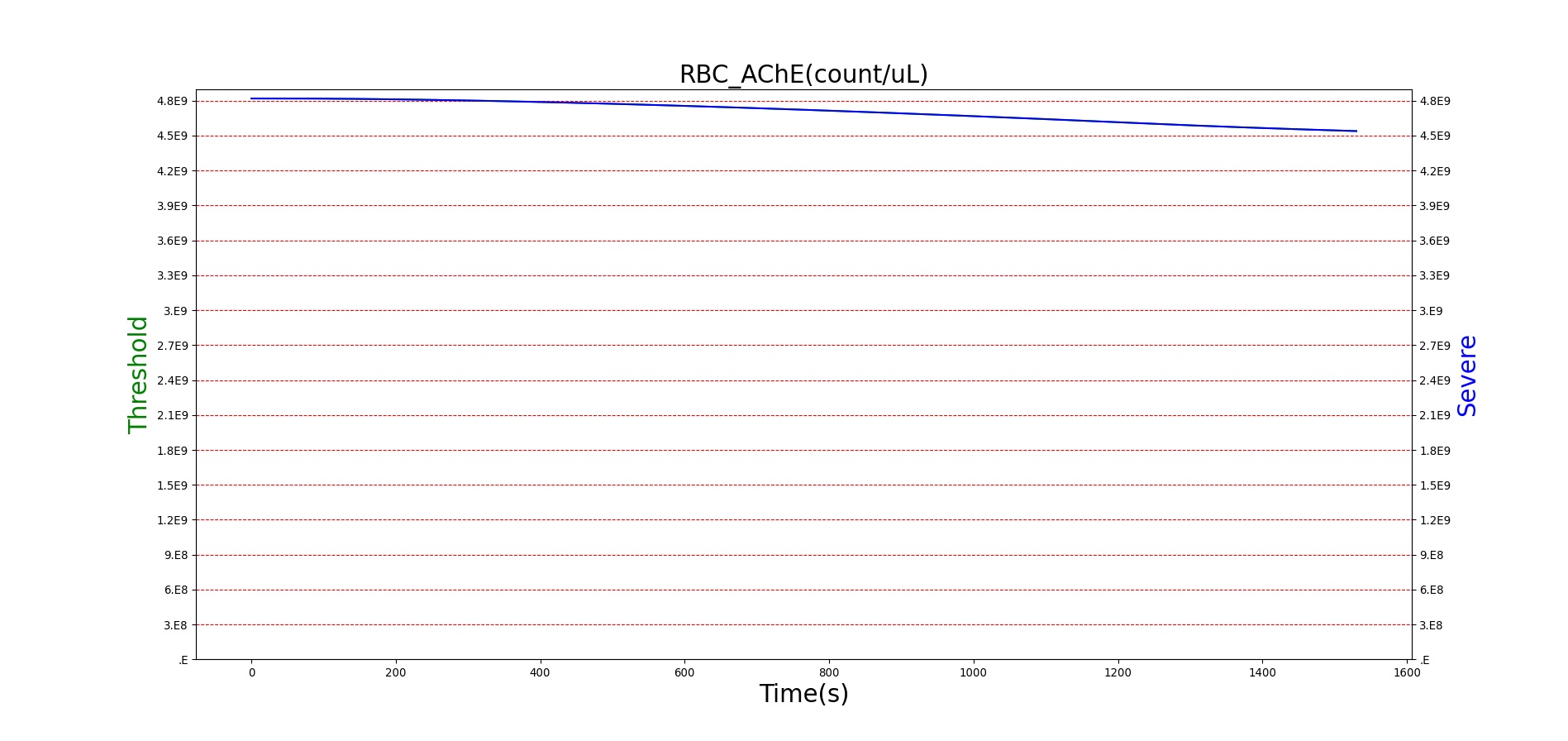
Since it is so toxic at low concentrations, the generic Emax model applied to other BioGears drugs is not readily extendable to Sarin. We instead model the interaction of Sarin with acetylcholinesterase directly. In particular, we describe the binding of Sarin to red blood cell acetylcholinesterase (RBC-AChE). Erythrocyte-bound AChE plays no role in the nervous system and is instead thought to act as a buffer for anti-acetylcholinesterase agents [24]. However, RBC-AChE is easier to assay than neuromuscular AChE and the relative activity of RBC-AChE has been reported to be moderately correlated with organophosphate symptomology [381]. Thus, we can feed the fraction of RBC-AChE inhibited to our pharmacodynamics model. It should be noted that, in practice, high variability in RBC-AChE activity in humans limits the effectiveness of this approach from a diagnostic viewpoint. Symptoms can appear without apparent RBC-AChE inhibition and 100% inhibition can occur with only mild symptoms [381]. However, such a caveat is not as concerning from a pure modeling standpoint.

The kinetic equations governing Sarin inhibition of AChE are given below with the following conventions: S = Sarin, A = acetylcholinesterase (erythrocyte bound), SA = sarin-acetylcholinesterase complex, X = aged (permanently deactivated) AChE, and P = Pralidoxime. Note that Sarin and Pralidoxime clearances are not stated because they are handled by existing BioGears functionality. Also note that Pralidoxime interaction with the Sarin-AChE complex follows Michaelis-Menten kinetics and that the resulting Sarin-Pralidoxime complex is not explicitly tracked. Initial concentrations of all species except RBC-AChE are assumed to be 0. According to the literature, an initial RBC-AChE of 8.0 nM can be expected [24]. Rate constants were obtained from [24], [289], and [125]. The constants k_syn and k_deg, which respectively represent basal synthesis and degradation of RBC-AChE, do not greatly impact the model but are included for completeness. Sarin is assumed to reach the bloodstream via the lungs after inhalation (the most likely route of exposure given the high volatility of Sarin) [290]. The particle-size histogram of aerosolized Sarin was adjusted to achieve a plasma concentration consistent with those observed in animal studies (for more on the methodology of inhaled particles in BioGears, see the Aerosol Section). Sarin is introduced to the simulation via an Environment Change (see Environment Actions).

\[\frac{d[S]}{dt} = -k_{S}*[S][A] \]

Equation 13.

\[\frac{d[A]}{dt} = -k_{S}*[S][A]-k_{deg}[A]+k_{syn}+\frac{k_{r}[SA][P]}{K_{D}+[P]} \]

Equation 14.

\[\frac{d[SA]}{dt} = k_{S}*[S][A]-k_{age}[SA]-\frac{k_{r}[SA][P]}{K_{D}+[P]} \]

Equation 15.

\[\frac{d[X]}{dt} = k_{age}[SA] \]

Equation 16.

\[\frac{d[P]}{dt} = -\frac{k_{r}[SA][P]}{K_{D}+[P]} \]

Equation 17.

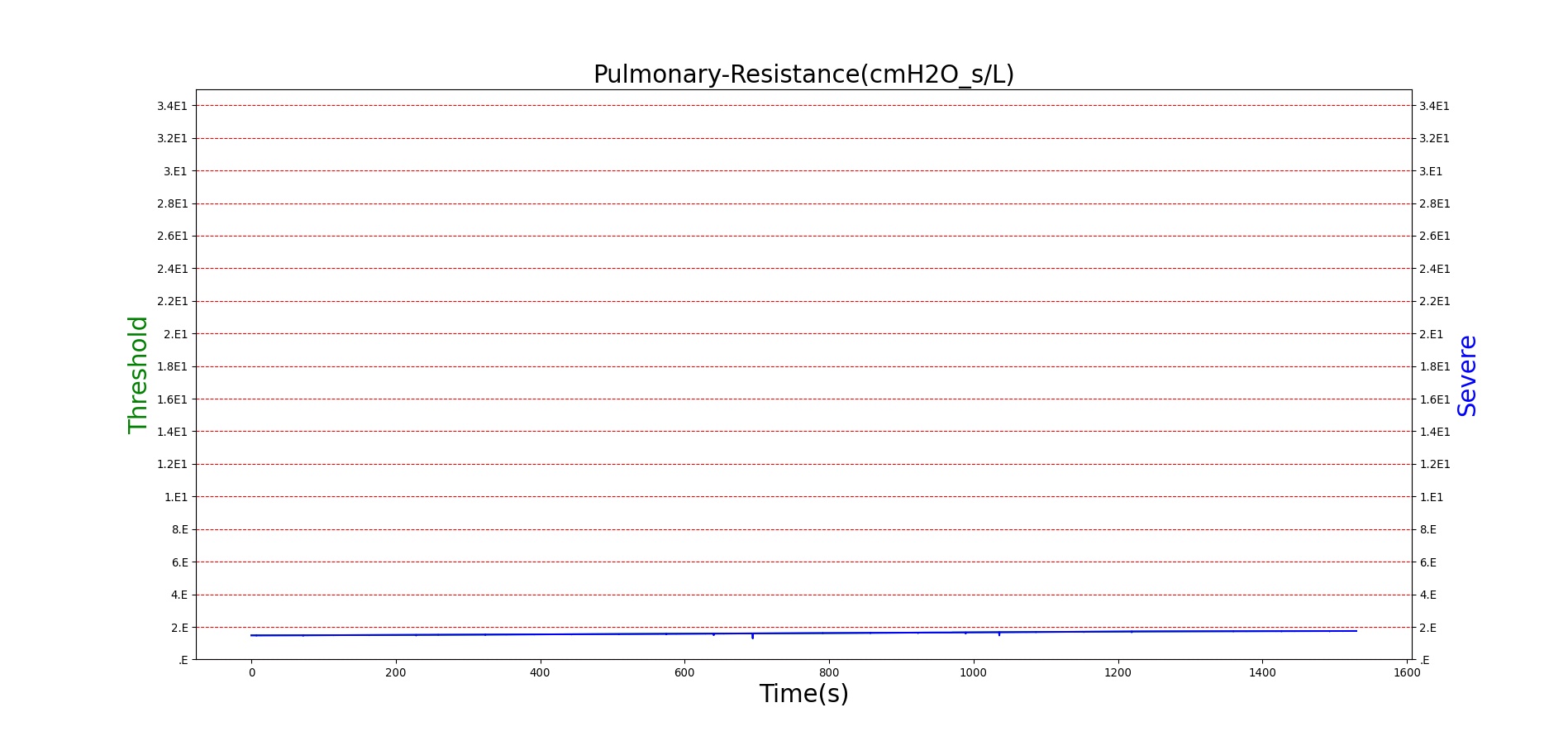
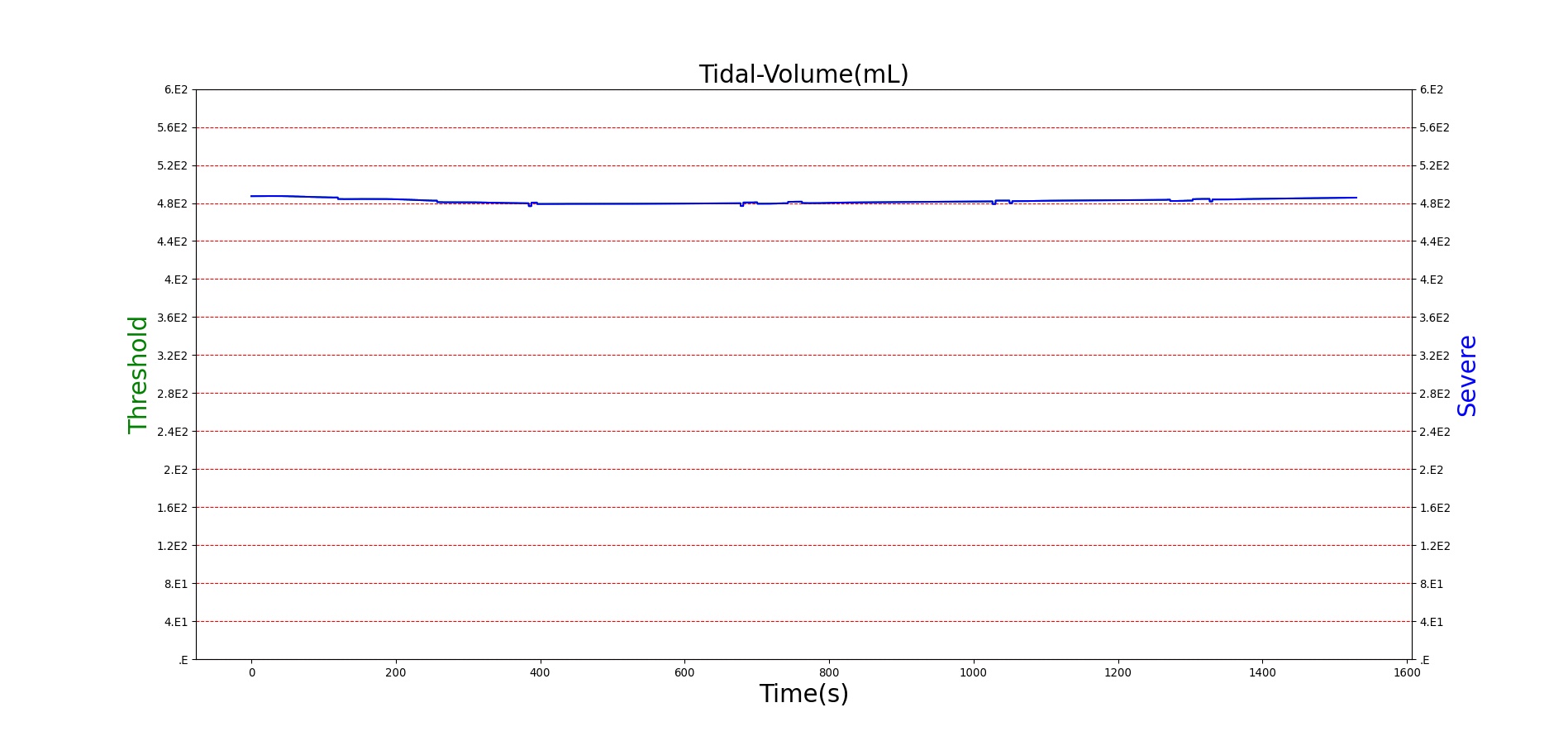
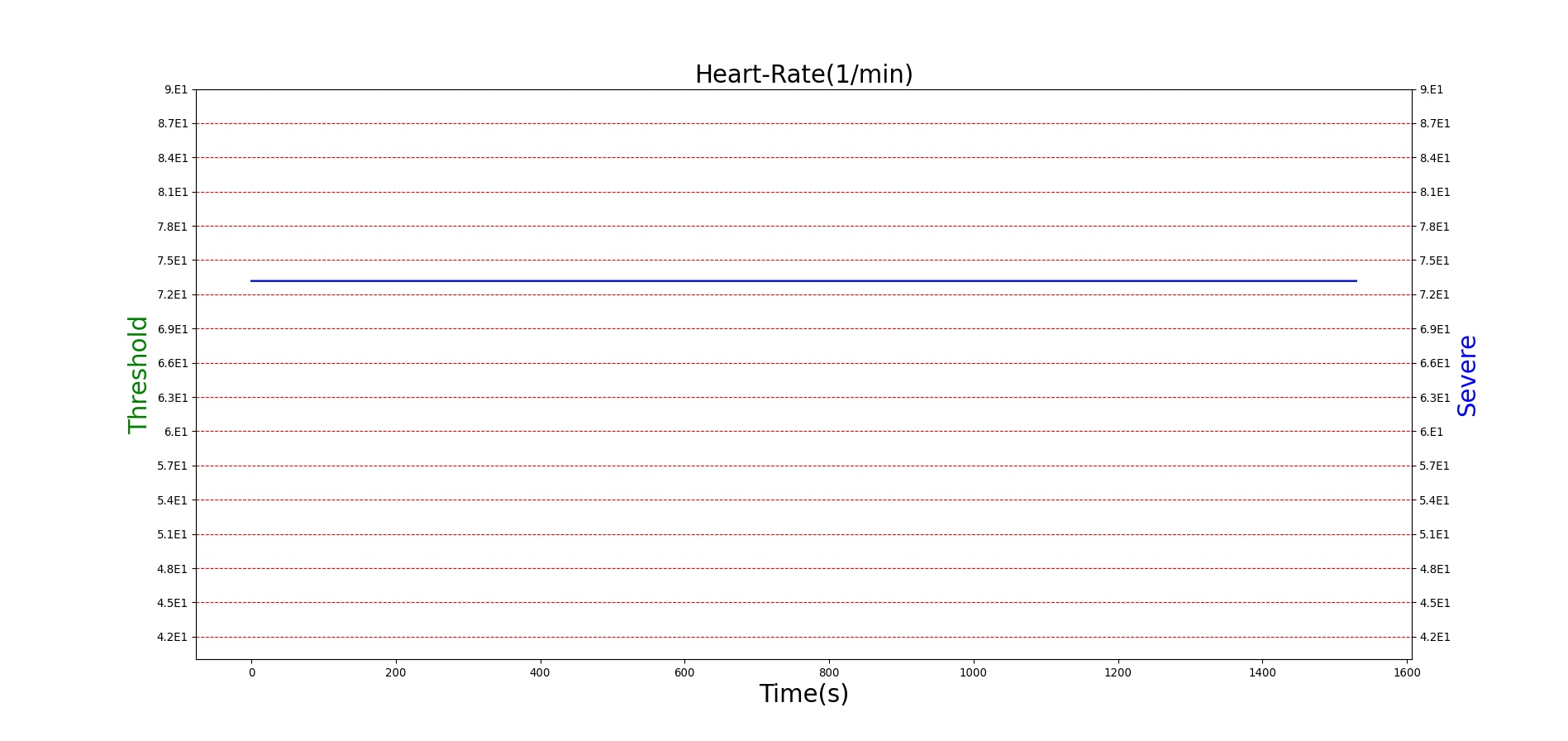
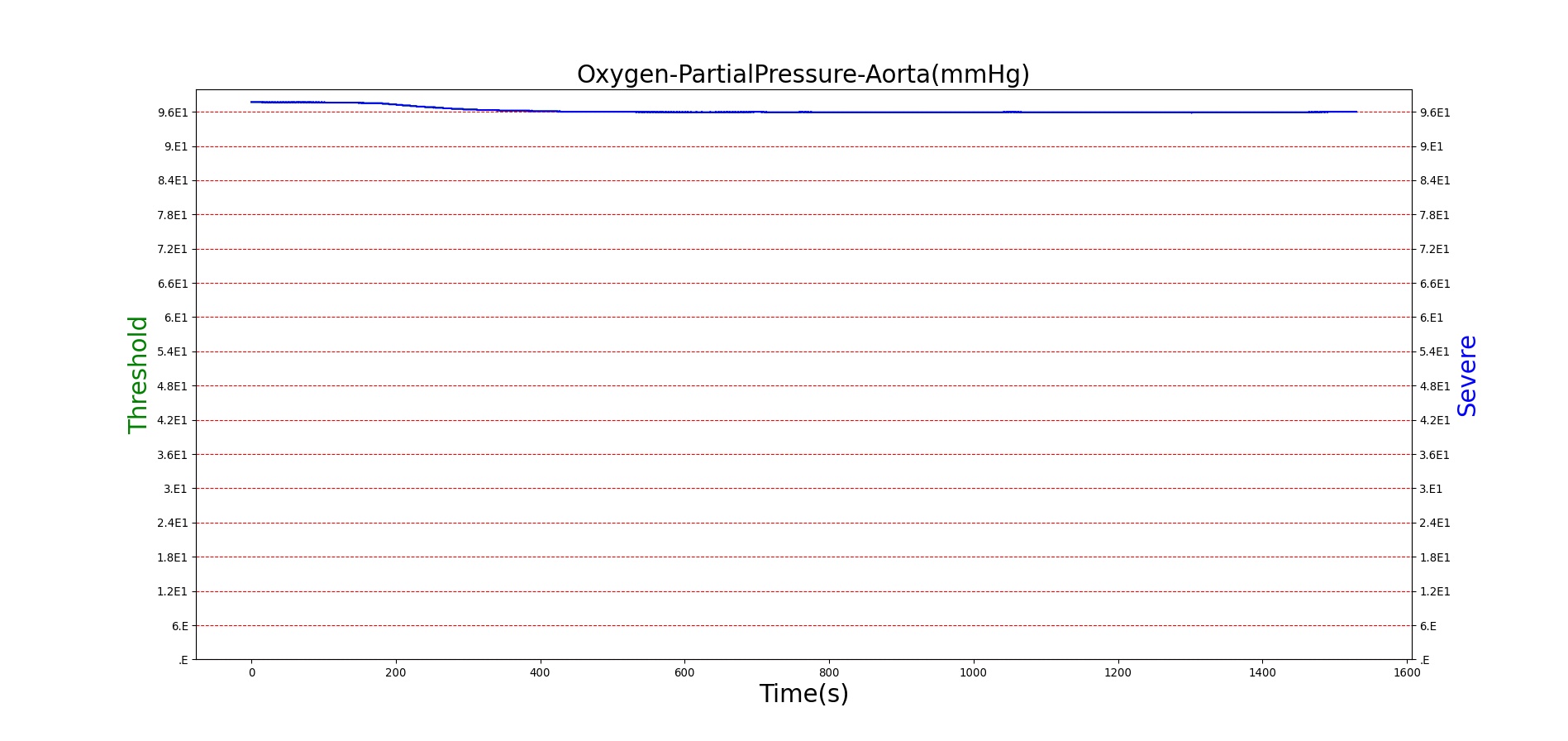
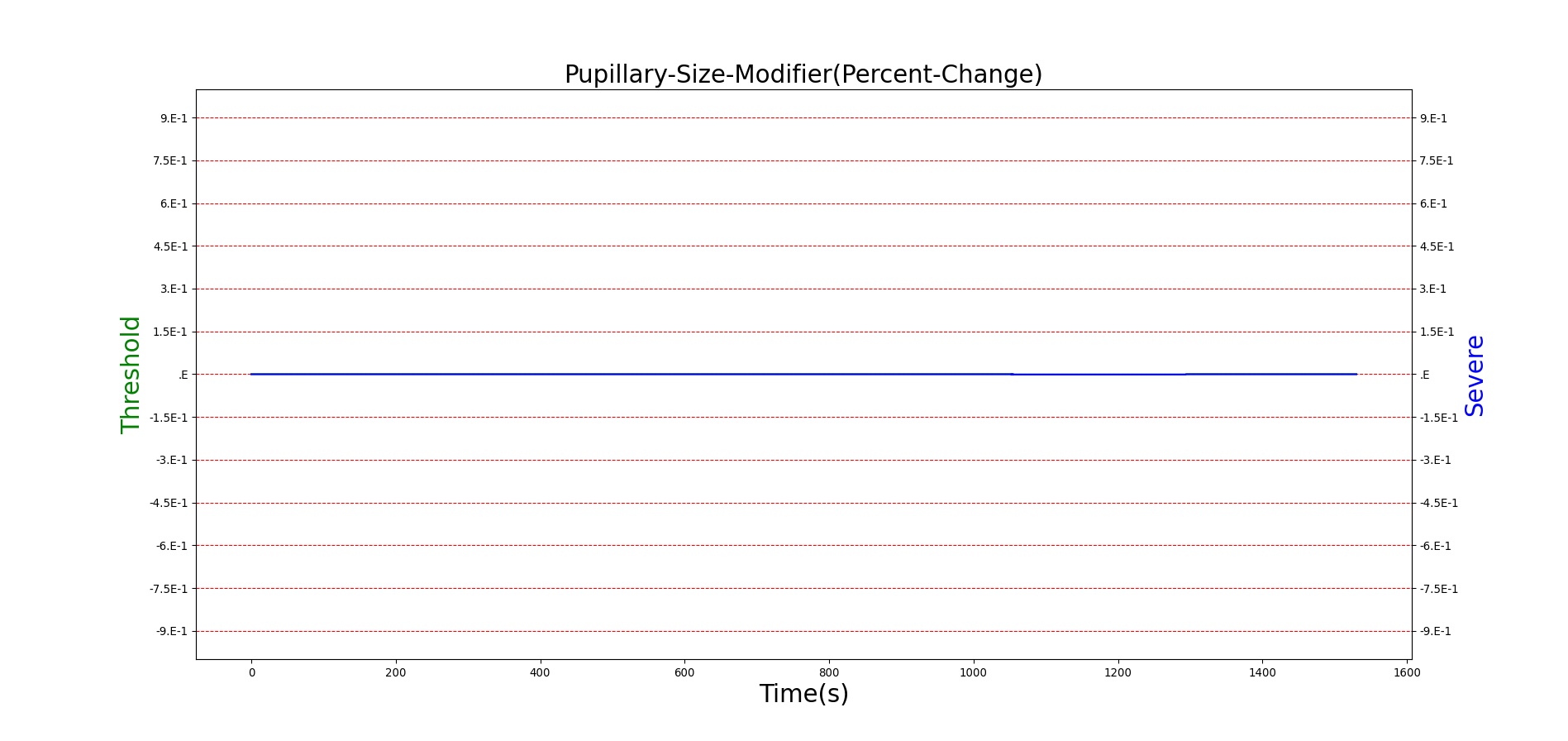
For reasons that are hopefully obvious, the validation metrics for Sarin exposure in humans (Tables 12 and 13) are predominantly qualitative. Estimates for the degree of RBC-AChE inhibition are either extrapolated from studies involving extremely low concentrations or drawn from case studies of accidental exposures. Figure 25 compares the predicted physiological responses to threshold and severe exposures. Figure 26 highlights the RBC-AChE salvaging action of Pralidoxime.

Table 11: Scenarios for Five Levels of Exposure to Sarin via Inhalation Ranging from Threshold (Mild Physiological Effects) to Lethal

Scenario	Notes	Occurrence Time (s)	Sampled Scenario Time (s)	Red Blood Cell Acetylcholinesterase Activity	Pupil Size	Respiratory Function	Cardiovascular Function	Blood Chemistry
Threshold Sarin Aerosol, Concentration = 0.2 mg/m^3	20 minute exposure; CT = 4 mg-min/m^3	30	1200	Slightly decreased [241]	~50% diameter reduction [55]	Mild bronchoconstriction [24]	Little to no change [55]	Little to no change [55]
Moderate Sarin Aerosol, Concentration (Short) = 5.0 mg/m^3	3 minute exposure; CT = 15 mg/m^3	30	1100	40-50% inhibited [24]	> 90% diameter reduction [55]	Respiratory discomfort [323] (quantified by Pulmonary Resistance Increase)	Little to no change	Little to no change
Moderate Sarin Aerosol, Concentration (Long) = 0.5 mg/m^3	30 minute exposure; CT = 15 mg/m^3	30	2700	40-50% inhibited [24]	> 90% diameter reduction [55]	Respiratory discomfort [323] (quantified by Pulmonary Resistance Increase)	Little to no change	Little to no change
Severe Sarin Aerosol, Concentration = 4 mg/m^3	10 minute exposure; CT = 40 mg-min/m^3	30	1500	75-80% inhibited [24]	Maximum constriction	Depressed ventilation; decreased tidal volume [416]	Bradycardia and decreased MAP [150]	Increased increased PCO2 and decreased P02 [416]
Lethal Sarin Aerosol, Concentration = 15 mg/m^3	6 minute exposure; CT = 90 mg-min/m^3	30	1050	100% inhibited	Maximum constriction	Fatal Respiratory Distress [26]	Bradycardia and decreased MAP [150]	Increased PCO2, Decreased PO2 (Hypercapnia & Hypoxia) [416]

Figure 25. Predicted responses to threshold (red) and severe (blue) exposures to Sarin inhaled from the environment. Note that constriction of the pupils (miosis) occurs even at very low Sarin concentrations. The difference in Pulmonary Resistance is due to deposition of Sarin in the upper respiratory tract, which leads to bronchoconstriction and difficulty breathing. As bronchoconstriction increases, the patient has trouble breathing deeply, resulting in a decrease in tidal volume.

Table 13: A severe inhaled dose of Sarin followed by intravenous administration of Pralidoxime

Action	Notes	Occurrence Time (s)	Sampled Scenario Time (s)	Red Blood Cell Acetylcholinesterase Activity	Pupil Size	Respiratory Function	Cardiovascular Function	Blood Chemistry
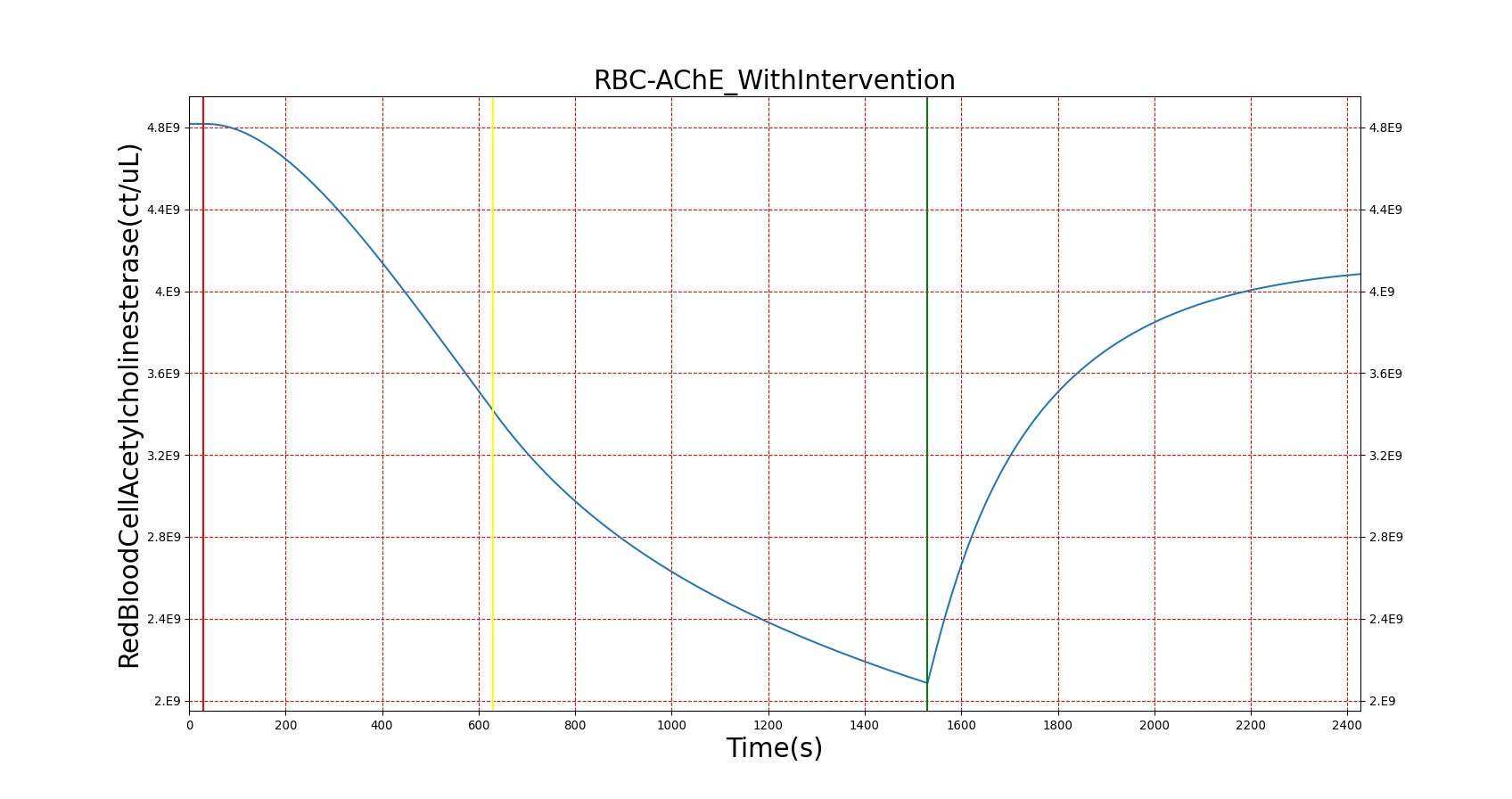
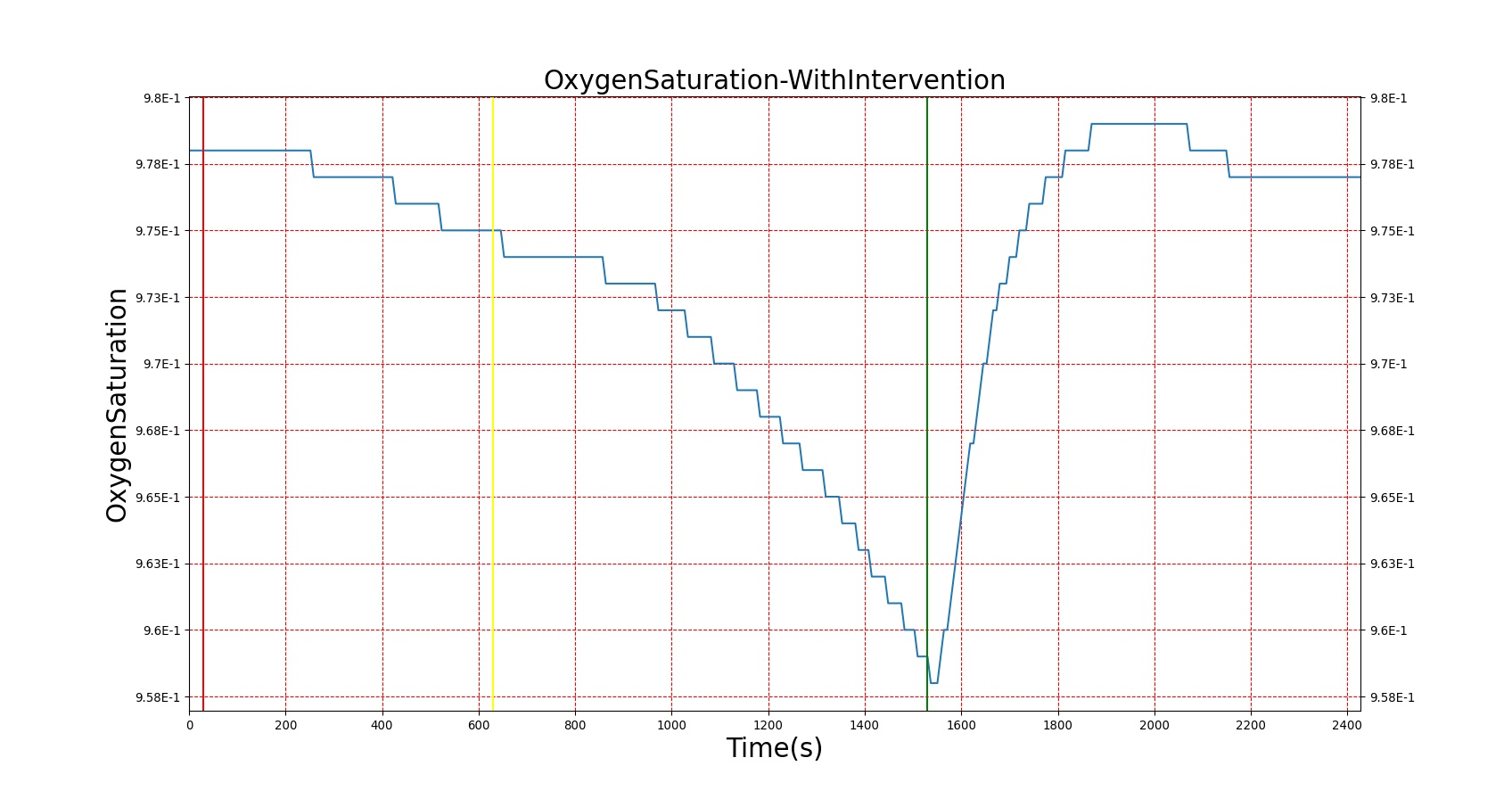
Severe Sarin Aerosol, Concentration = 20 mg/m^3	2 minute exposure; CT = 40 mg-min/m^3	30	1530	75-80% inhibited [24]	Maximum constriction	Depressed ventilation; decreased tidal volume [416]	Bradycardia and decreased MAP	Increased increased PCO2 and decreased P02
Pralidoxime 15mg/kg Iv [24]		1530	2430	Increase in activity [323]	No change	Increased respiration rate [304]	Increased heart rate [304]	Decreased PCO2 and increased PO2

Figure 26. A severe Sarin exposure (green line = beginning of exposure, black line = end of exposure) followed by administration of 1 g intravenous Pralidoxime (pink line). The red blood cell acetylcholinesterase levels increase, though not to baseline because a fraction of the RBC-AChE still undergoes irreversible aging. The oxygen saturation is shown to demonstrate the positive effect that Pralidoxime has on respiratory function

Conclusions

In general, the drugs in the BioGears library have strong agreement with both the published data and subject matter expertise. The biggest limitation lies in the transient response to drugs. Currently, the system tolerances provide a response within 30–60 seconds for all drugs, regardless of the physiologic onset time. The drug response also wears off quickly for all drugs. It is difficult to specify the desired pharmacodynamic response without a well thought out set of parameters. These issues will be addressed as part of future work on the BioGears Engine by validating the pharmacokinetic model and implementing and validating a pharmacodynamic model.

These models and the combination of these models represent a positive step forward for drug simulation. The parameters are intuitive and accurate for each drug and additional drugs can be added for an expanded drug library.

Future Work

Coming Soon

• Intoxication models for drugs beyond Morphine
• Expanded drug library
• Integration of receptor-based pharmacodynamics
• Multiple types of drug-drug interactions

Recommended Improvements

• Long-term drug effects, including physiological changes
• Additional drugs
• Improved kinetic model for aerosols and vapors
• Higher fidelity models of other routes, including epithelial cell (integumentary, gastrointestinal) absorption
• Drug sensitivity variation

Appendices

Acronyms

MAP - Mean Arterial Pressure

PK - Pharmacokinetic

PD - Pharmacodynamic

SDK - Software Development Kit

SMEs - Subject Matter Experts

Data Model Implementation

Drug