Overview
Abstract
The BioGears Nervous System models the central nervous system (CNS) and peripheral nervous system (PNS). Currently, the system models afferent signal generation as a result of baroreceptor, chemoreceptor, lung-strech receptor activity. These signal are processed by a rudimentary central nervous system (CNS) that relays commands to efferent effectors. Additionally, the Nervous System provides tracks parameters related to traumatic brain injury events, pain stimulus response, and drug effects. In the future, other feedback mechanisms will be added for improved modeling of homeostatic and crisis states.
Introduction
The Nervous System in the human body is comprised of the central nervous system (CNS) and the the peripheral nervous system (PNS). The CNS contains the brain and the spinal cord, while the PNS is subdivided into the somatic, autonomic, and enteric nervous systems. The somatic system controls voluntary movement. The autonomic nervous system is further subdivided into the parasympathetic and sympathetic nervous system. The sympathetic nervous system is activated in times of stress and crisis, commonly referred to as the "flight or fight" behaviors. The parasympathetic nervous system controls homeostasis functions during the relaxed state. The enteric nervous system controls the gastrointestinal system. Many of these behaviors are tightly connected to the Endocrine System. In many cases, the Nervous System receptors trigger hormone releases that cause systemic changes, such as dilation and constriction of vessels, heart contractility changes, and respiration changes [134].
BioGears will focus on a select few mechanisms within the Nervous System to provide feedback for both homeostasis and crisis behavior in the body. The list is shown below:
- Baroreceptors (aortic, carotid, and low-pressure)
- Chemoreceptors
- Pulmonary stretch receptors
- Local autoregulation
- Temperature Effects
- Generic parasympathetic and sympathetic effects
- Pain stimulus
- Sleep and sleep deprivation
Additionally, BioGears will model the following features related to brain function:
- Simple model of traumatic brain injury (TBI)
- Intracranial pressure
- Pupillary response to drugs and TBI
System Design
Background and Scope
The BioGears Nervous System began as a low-fidelity model that tracked metrics associated with brain injury. Over time, feedback models local to other BioGears systems (i.e. baroreceptors, chemoreceptors) were relocated to the Nervous System with the goal of moving towards a centralized Nervous model that serves as a global controller. The primary difficulty with such a model is that most detailed Nervous models rely on differential equations that output nerve firing rates. If the frequencies of these firing rates are too high compared to the time-step used to model the equations, the solution will be unstable. Fortunately, as BioGears stability has been improved, the simulation time-step has been decreased to its current value of 0.02 s. This step size allowed us to work toward strengthenging the interactions between the existing models.
Data Flow
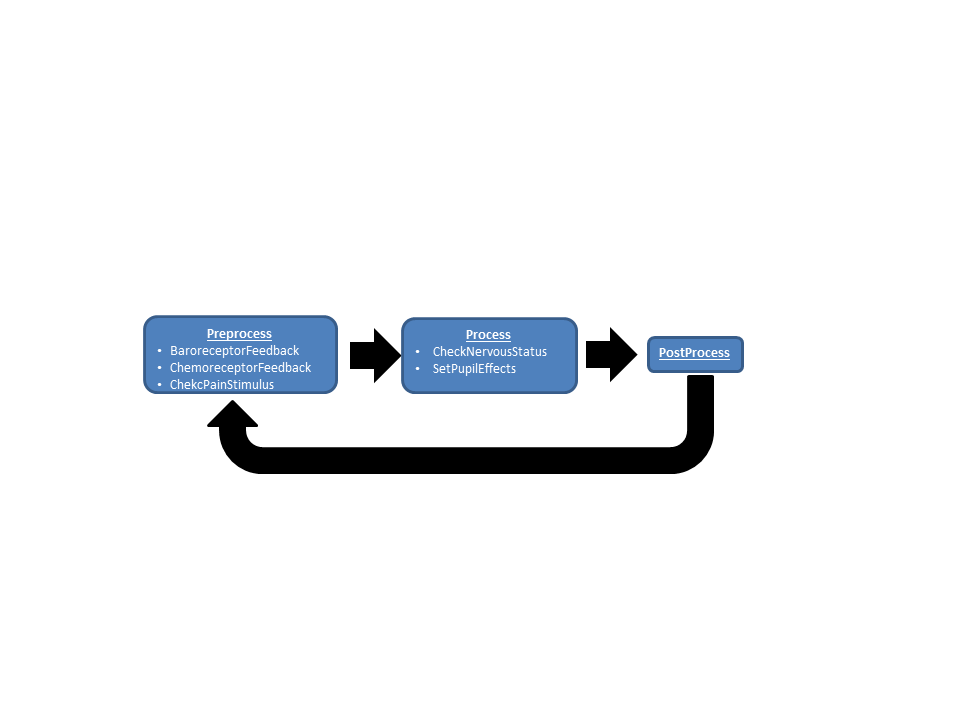
An overview of the data flow in the BioGears Nervous system is shown in Figure 1.
Initialization and Stabilization
The BioGears initialization and stabilization is described in detail in the stabilization section of the System Methodology report. Setpoints related to Nervous model are reset once the Cardiovascular system reaches a homeostatic state. These include the baseline baroreceptor operating pressure, the baseline oxygen and carbon dioxide blood gas levels, the baseline sympathetic and parasympathetic firing rates, and the baseline cerebral blood flow.
Preprocess
Afferent Signal Generation
This method surveys the current state of the patient (blood pressure, blood-gas levels, lung capacity) and relays information to the central nervous system.
Baroreceptor Feedback
The baroreceptor mechanism provides rapid negative feedback control of arterial pressure. A drop in arterial pressure is sensed by the baroreceptors and leads to an increase in sympathetic activity and vagal (parasympathetic) withdrawal. These changes operate with the goal of maintaining arterial pressure at its healthy resting level. BioGears distinguishes between aortic, carotid, and low-pressure (cardiopulmonary) receptors. Aortic and carotid receptors are both sensitive to changes in systolic arterial pressure, but their relative locations in the body affect this response. Aortic baroreceptors respond to the transmural pressure between the aorta and the intrapleural space. The carotid baroreceptors, located a distance above the heart, are affected by pressure head (except when an individual is lying down). Low-pressure receptors are located near the venous return to the heart and are therefore sensitive to the central venous pressure and pleural pressure. BioGears uses a stress-strain relationship to calculate the signal generated at the aortic and carotid baroreceptors [272] and a first-order, low-pass filter to generate the low-pressure receptors signal [183].
Chemoreceptor Feedback
The chemoreceptor mechanism provides feedback control to regulate the partial pressures of oxygen and carbon dioxide in the blood. The response is divided in to two components: peripheral and central. Peripheral chemoreceptors (which reside in the aortic arch and carotid arteries) are sensitive to deviations in both oxygen and carbon dioxide pressures. The central chemoreptors, so named because of their location in the central nervous system, respond only the carbon dioxide pressure changes. Assuming that each receptor class operates independently, the feedback from the central and peripheral chemoreceptors is summed to generate changes in respiration frequency and respiratory driver pressure to restore blood gas levels to their set points. The peripheral chemoreceptor signal is also processed by the central nervous model to account for its contribution to cardiovascular activity.
Pulmonary Stretch Receptors
Stretch receptors respond to changes in lung volume. They tend to balance the cardiovascular effects induced by peripheral chemoreceptors [360].
Central Nervous (CNS) Response
This method consolidates the signals generated by the afferent models and adjusts the relative firing rates of the sympathetic and parasympathetic arms of the nervous system. The sympathetic signal consists of two outputs: a sinoatrial portion that affects heart rate and elastance and a peripheral portion that affects systemic resistance and unstressed venous volume. The parasympathetic signal only acts upon the heart rate. The threshold for sympthetic firing is lowered under hypoxic conditions to model the ischemic response [360].
Efferent Response
The efferent response carries out the work of updating the state of the cardiovascular system according to the autonomic response determined by the CNS. This model determines the normalized changes in heart rate, heart elastance, peripheral vessel resistance, and peripheral venous compliance. The peripheral resistance response distinguishes between the splanchnic, extrasplanchnic, and skeletomuscular regions of the body to account for preferential blood-flow shunting during certain extreme responses (e.g. maintaining flow to vital organs during hemorrhage).
Local Autoregulation
The brain, muscle, and myocardium prioritize blood flow and oxygen delivery. BioGears models cerebral autoregulation in which vessels in the brain constrict or dilate to maintain constant cerebral blood flow, perfusion pressure, and oxygen saturation. BioGears also models local regulation in the vessels of the muscle and myocardium in which vasodilation occurs in response to oxygen depletion.
Check Pain Stimulus
Pain can be initiated in BioGears via a Pain Stimulus action. The BioGears pain response takes into account both the magnitude of the pain action and the susceptibility of the virtual patient to pain (set in the Patient definition file). The result is an output corresponding to the pain Visual Analog Scale (VAS) on a 0-10 interval. The VAS score dictates the patient cardiovascular and respiratory response to the pain stimulus. Increased epinephrine production is also stimulated.
Calculate Sleep Effects
As a patient becomes more and more sleep deprived many physiological factors begin to become manifest in the body. Notabley, control of hormone function becomes greately deminished as a function of sleep deprivation. BioGears models this disregulation as the patient is awake for a prolonged period of time. This is of particular importance in prolonge field care scenarios where evacuation to higher levels of care may be denied for up to 72 hours. In these intances, if the patientes sleep isn't managed properly, insuluin synthesis will become greatly dimished, resulting in hyperglycemia. In addition, BioGears now provides access to the psychomotor vigilance task patient assesment which will allow the care provider to determine sleep debt through analysis of reaction time and lapses in attention while performing a focused task.
Process
Check Nervous Status
Events associated with nervous system functionality are evaluated. First, intracranial pressure is checked to determine whether or not to throw the Intracranial Hypertension or Intracranial Hypotension events. Then, the presence of fasciculation (muscle spasms) is evaluated based on the activity of the compounds Sarin and Succinylcholine. The latter drug generally produces transient fasciculation which disappear when neuromuscular block is achieved [11]. For a description of the neurological effects of Sarin, see the Nerve Agent: Sarin section in the Drugs documentation. It should be noted that fasciculation can also be caused by an ion imbalance; however, this functionality is not yet active. When completed, the criteria for this type of event will be calcium deficiency. If the patient's arterial calcium concentration falls below one milligram per deciliter, then fasciculation will be triggered [128].
SetPupilEffects
Pupil modifiers are retrieved from the Drugs System and combined with any modifiers from TBI before being applied to the eyes.
Post Process
There is no system specific functionality for the Nervous System in Post Process.
Assessments
Assessments in BioGears are data collected and packaged to resemble a report or analysis that might be ordered by a physician. No BioGears assessments are associated with the Nervous System.
Features, Capabilities, and Dependencies
Baroreceptors
BioGears calculates the strain exerted on the aortic and carotid baroreceptors as [272]
\[ \epsilon_{w} = 1 - \sqrt{\frac{1 + \exp(-q_w\left(P_{input} - s_w\right))}{A+\exp(-q_w\left(P_{input}-s_w\right))}} \]
The input pressure (Pinput) is the systolic arterial pressure (Psys) for the carotid baroreceptors and the difference between systolic pressure and pleural pressure (Psystolic - Ppleural) for aortic baroreceptors. The parameters for Equation 1 are maximum stressed to unstressed vessel cross-sectional area (A), steepness (qw), and operating point (sw) and the output is wall strain (εw). As described in the cardiovascular methodology report, theBioGears cardiovascular system is initialized according to patient definitions and stabilized to a homeostatic state. The baroreceptor operating pressure is the systolic pressure following the engine stabilization period. This operating point is adjusted dynamically with certain actions and insults, as shown in Equation 2.
\[ s_w = P_{sys, set} + \Delta P_{drugs} + \Delta P_{exercise} + \Delta P_{pain} \]
Where Δpdrugs, Δpexercise, and Δppain are changes in apparent operating point due to certain drugs, exercise, and pain response. It is known that aortic and carotid baroreceptors adapt to sustained changes in arterial pressure. We model adaptation by adjusting the operating point as a function of systolic arterial pressure [266]
\[ \frac{ds_w}{dt} = k_{adapt}\left(P_{sys} - s_w\right) \]
.
The value of kadapt reflects a half-time of approximately 16 hours for the baroreceptors to acclimate to a sustained step-change in systolic pressure [266].
The baroreceptors are assumed to operate as a spring-dashpot system. The strain induced by the stress $ $ is determined by the differential equation [272]
\[ \frac{d \epsilon_{b}}{dt} = \frac{-\epsilon_{b} + K_b \epsilon_{w}}{\tau_{b}} \]
The strain signal εb determined for each baroreceptor class (aortic and carotid) is processed in the Central Nervous response.
The low-pressure baroreceptor signal is generated by sampling the transmural pressure between the venous return (CVP) and the pleural space [183].
\[ \frac{d\tilde{P_{cp}}}{dt} = \left(\frac{1}{\tau_{cp}}\right)\left(-\tilde{P_{cp}} + \left(CVP - P_{pleural}\right)\right) \]
\[ f_{cp} = \frac{f_{cp,max}}{1.0 + \exp(\left(CVP_{base} - P_{pleural,base}\right) - \tilde{P_{cp}})} \]
Equation 5 acts as a low-pass filter that reduces signal noise and Equation 6 generates a firing rate (fcp) that is processed by the CNS. τcp and fcp,max are the time constant for the response and the maximum firing rate, while CVPbase and Ppleural,base represent the normal central venous and pleural pressures.
Chemoreceptors
The chemoreceptors are cells that are sensitive to changes in blood gas concentration. Peripheral chemosensitive cells–located in the aortic arch–detect fluctuations in both arterial carbon dioxide and oxygen partial pressures. The central chemoreceptors, which reside in the central nervous system (CNS), respond to changes in cerebral blood pH caused by irregular carbon dioxide levels. It is assumed in this model that carbon dioxide transport across the blood-brain barrier and equilibration therein are rapid processes; that is, it assumed that the central chemoreceptor response is proportional to deviations in arterial carbon dioxide.
Control of respiration is based on the model developed by Albanese, Magosso, and Ursino in [360], [198], [362], and [5]. It is assumed that the central (c) and peripheral (p) feedback define deviations from baseline patient respiration frequency (f) and peak respiratory driver pressure (Pmax), and that their contributions are independent (and thus additive).
\[f_{target} = f_{base} + \Delta f_c + \Delta f_p \]
\[P_{max,target} = P_{max,base} + \Delta P_{max,c} + \Delta P_{max,p} \]
Clearly, the blood gas levels are normal, central Vc and peripheral Vp changes in ventilation are 0, and target ventilation Vtarget equals patient baseline ventilation Vbase.
The evolution of the central chemoreceptor feedback is assumed to be a function of arterial carbon dioxide partial pressure (PCO2) deviation from its normal set point (PCO2,set = 40 mmHg).
\[ \frac{d\Delta E_{c}}{dt} = \left(\frac{1}{ \tau_{E,c}} \right) \left( -\Delta{E_{c}} + g_{E,c}\left(P_{CO_{2}}(t) - P_{CO_{2,set}}\right)\right) \]
The effects (E) are frequency (f) and driver amplitude (P) with associated time constants (τc) and controller gains (τgc). Equation 9 is identical to that reported in [5], except that a delay term is omitted. This omission is a result of being currently unable to model delay differential equations in BioGears.
The form of the peripheral feedback in Equation 10 is similar to Equation 8, but the response is dictated by the combined effects of carbon dioxide pressure and oxygen saturation. Equations 11-12 show how this firing rate (f(t)) is calculated. As before, this equation is applied twice per effect (E = {f, P}).
\[ \frac{d\Delta E_{p}}{dt} = \left(\frac{1}{ \tau_{E,p}} \right) \left( -\Delta E_{p} + g_{E,p}\left(f(t) - f_{set}\right)\right) \]
\[ \frac{df}{dt} = \frac{1}{\tau_{f}}\left(-f(t) + \psi\right) \]
\[ \psi = \frac{f_{max} + f_{min}*exp\left(\frac{P_{O_{2}} - P_{O_{2,half}}}{k_{O_{2}}}\right)}{1 + exp\left(\frac{P_{O_{2}} - P_{O_{2,half}}}{k_{O_{2}}}\right)}*\left[K*ln\left(\frac{P_{CO_{2}}}{P_{CO_{2,set}}}\right) + \gamma\right] \]
Equation 12 is a sigmoid that outputs a chemoreceptor firing rate (bounded by fmin and fmax) based on the current arterial oxygen pressure (PO2). The variables PO2,half and kO2 are the half-max and slope parameters that define the shape of the sigmoid, a shape which is increasingly adjusted as the arterial carbon dioxide pressure (PCO2) deviates from normal (PCO2,set). K and γ are tuning parameters required to maintain a steady output when oxygen and carbon dioxide pressures are at their normal values. Values for all parameters in Equations 9-12 are available in [198].
Pulmonary Stretch Receptors
Pulmonary stretch receptors are modeled as in [360], except that total lung volume (Vlung) is used as the input rather than tidal volume. We make this change because the total lung volume in BioGears is a more stable output than tidal volume.
\[ \frac{df_{ps}}{dt} = \frac{-f_{ps} + G_{ps}V_{lung}}{\tau_{ps}} \]
Central Nervous Response
The CNS model outputs three signals: a sympathetic efferent signal to the sinoatrial node (fes,s), a sympathetic efferent signal to the periphery (fes,p), and an efferent vagal (parasympathetic) signal to the sinoatrial node (fev). These signals are determined by weighting the following inputs from the afferent arm of the nervous system: aortic baroreceptors (fab), carotid baroreceptors (fcb), cardiopulmonary baroreceptors (fcp), peripheral chemoreceptors (fpc), and pulmonary stretch receptors (fps). The equations for the three efferent signals have been developed in [360], [198], [199], and [5]. Weighting parameters (Wj) were established from these sources as well as from [183] and [182].
The sympathetic efferent firing rates are modeled as sigmoids:
\[ f_{es,s} = f_{es,\infty} + \left(f_{es,0} - f_{es,\infty}\right)exp(k_{es}\left(W_{s,ab}f_{ab} + W_{s,cb}f_{cb} + W_{s,pc}f_{pc} + W_{cp}\left(f_{cp} - f_{cp,0}\right) - \theta_{s}\right)) \]
\[ f_{es,p} = f_{es,\infty} + \left(f_{es,0} - f_{es,\infty}\right)exp(k_{es}\left(W_{p,ab}f_{ab} + W_{p,cb}f_{cb} + W_{p,pc}f_{pc} + W_{p,ps}f_{ps} + W_{cp}\left(f_{cp} - f_{cp,0}\right) - \theta_{p}\right)) \]
The parameters θs and θp refer to the firing thresholds of the sinoatrial and peripheral sympathetic signals. These thresholds are adjusted under hypoxic and hypercapnic scenarios to model the ischemic response [198].
\[ \frac{d\Delta\theta_{O_2,j}}{dt} = \frac{1}{\tau_{isc}}\left(-\Delta\theta_{O_2,j} + \frac{\chi_{j}}{1+\exp(\frac{P_{O_2}-h_{O_2,j}}{k_{isc,j}})}\right) \]
\[ \frac{d\Delta\theta_{CO_2,j}}{dt}= \frac{-\theta_{CO_2,j}+g_{c,j}\left(P_{CO_2}-P_{CO_2,n}\right)}{\tau_c} \]
\[ \theta_{j} = \theta_{j,n} - \Delta\theta_{O_2,j} - \Delta\theta_{CO_2,j} \]
In Equations 16-18, the subscript "j" refers to either the sinoatrial or peripheral ischemic response. The parameters θj,n refer to the basal values the thresholds take on at normal blood-gas levels. The maximum slope and half-saturation parameters (hO2,j and kisc, respectively) determine the overall shape of the response.
The parasympathetic signal is a sigmoidal function of the baroreceptor firing rate and linear with respect to the chemoreceptor and pulmonary stretch signals.
\[ f_{ev} = \left(\frac{f_{ev,0} + f_{ev,\infty}\exp(\frac{f_{b,avg}-f_{b,avg,0}}{k_{ev}})}{1+\exp(\frac{f_{b,avg}-f_{b,avg,0}}{k_{ev}})}\right) + W_{v,pc}f_{pc}+W_{v,ps}f_{ps} - \theta_{ev} \]
Unlike the sympathetic efferent pathway, the parasympathetic path assumes a constant firing theshold ({ev}). The value fb,avg is the average firing rate of the carotid and aortic baroreceptors. The low-pressure baroreceptors do not effect the parasympthetic signal.
Efferent Response
The three signals relayed by the CNS (fes,s, fes,p, and fev) are used to update the cardiovascular model using effector equations outlined in [360]. These equations have been normalized so that their outputs represent a fractional change from baseline. As in [360], the response to the sympathetic activation is assumed to involve a logarithmic transformation, whereas the vagal response is linear. Furthermore, the sympathetic signals are bounded at the minimum signal fes,min to maintain continuity. In each of the normalized equations, the values σ0 correspond to the effector input at the baseline sympathetic and parasympathetic firing rates.
Heart Rate
\[ \frac{d \sigma_{HR, s}}{dt} = \frac{-\sigma_{HR,s} + G_{HR,s}\ln(f_{es,s}-f_{es,min}+1}{\tau_{HR,s}} \]
\[ \frac{d \sigma_{HR, v}}{dt} = \frac{-\sigma_{HR,v} + G_{HR,v}f_{ev}}{\tau_{HR,v}} \]
\[ HR_{norm} = \frac{1 + \sigma_{HR,s,0} + \sigma_{HR,v,0}}{1 + \sigma_{HR,s} + \sigma_{HR,v}} \]
In Equation 22, the initial state of the heart rate appears in the numerator because Equations 21-22 reflect changes in heart period. Thus, inverting the ratio of next heart period to baseline heart period gives the normalized change in heart rate.
Heart Elastance
\[ \frac{d \sigma_{E}}{dt} = \frac{-\sigma_{E} + G_{E}\ln(f_{es,s}-f_{es,min}+1}{\tau_{E}} \]
\[ E_{norm} = \frac{1 + \sigma_{E}}{1 + \sigma_{E,0}} \]
Vessel Resistance
\[ \frac{d \sigma_{R,j}}{dt} = \frac{-\sigma_{R,j} + G_{R,j}\ln(f_{es,p}-f_{es,min}+1}{\tau_{R,j}} \]
\[ R_{j,norm} = \frac{1 + \sigma_{R,j}}{1 + \sigma_{R,j,0}} \]
In Equations 25-26, j = splanchnic, extrasplanchnic, or muscle. Each region has distinct controller gains and time constants associated with it.
Veinous Compliance
\[ \frac{d \sigma_{C}}{dt} = \frac{-\sigma_{C} + G_{C}\ln(f_{es,p}-f_{es,min}+1}{\tau_{C}} \]
\[ C_{norm} = \frac{1 + \sigma_{C}}{1 + \sigma_{C,0}} \]
The normalized compliance is applied to each fluid capacitor in the systemic portion of the BioGears cardiovascular circuit.
Local Autoregulation
Cerebral Autoregulation
The cerebral autoregulation model is based on that of [359] and [361]. The model distinguishes between changes in large arteries (upstream resistor in the BioGears cerebral circuit) and small arteries (downstream resistor). The large arteries respond to changes in cerebral perfusion pressure (CPP), while the small arteries are sensitive to changes in cerebral blood flow (CBF). Each response is attenuated by cerebral venous oxygen saturaton and cerebral carbon dioxide levels. In all equations, a subscript "n" refers to the normal, basal value of the parameter.
The response of large arteries to changes in CPP is governed by [359]
\[\frac{dx_{auto,l}}{dt} = \frac{-x_{auto,l} + G_{auto,l}\left(CPP - CPP_{n}\right)}{\tau_{auto,l}} \]
The response of small arteries to CBF is likewise given by [359]
\[\frac{dx_{auto,s}}{dt} = \frac{-x_{auto,s} + G_{auto,l}\left(\frac{CBF-CBF_n}{CBF_n}\right)}{\tau_{auto,s}} \]
The effects of carbon dioxide [359] and oxygen saturation [361] are tracked as follows:
\[\frac{dx_{CO_2}}{dt} = \frac{-x_{CO_2} + A_{CO_2}G_{CO_2}log_{10}\left(\frac{P_{CO_2}}{P_{CO_2,n}}\right)}{\tau_{CO_2}} \]
\[ A_{CO_2} = \left(1+\exp(-K_{CO_2}\left(\frac{CBF-CBF_n}{CBF_n}\right) - b_{CO_2})\right)^{-1} \]
\[\frac{dx_{O_2}}{dt} = \frac{-x_{O_2} + G_{O_2}\left(S_{v,O_2}-S_{v,O_2,n}\right)}{\tau_{O_2}} \]
The total autoregulatory effects used to scale the large and small cerebral resistances are:
\[ x_{large} = x_{auto,l} + x_{CO_2} + x_{O_2} \]
\[ x_{small} = x_{auto,s} + x_{CO_2} + x_{O_2} \]
Coronary and Skeletomuscular Autoregulation
Autoregulation in the heart and muscle is modeled similarly to [360]. The autoregulatory parameter for each location is:
\[ \frac{dx_{O_2,j}}{dt} = \frac{-x_{O_2,j} + G_{O_2,j}\left(C_{v,O_2,j}-C_{v,O_2,jn}\right)}{\tau_{O_2,j}} \]
where j is either the muscle or heart, Cv,O2 is the current venous oxygen concentration, and Cv,O2,n is the baseline venous oxygen concentration.
The change in resistance of the circuit path providing blood flow to the heart is
\[ R_{h} = \frac{R_{h,0}}{1 + x_{O_2,h}}\]
in which Rh,0 is the baseline resistance (constant). The expression describing the change in muscle resistance is similar to Equation 36.
\[ R_{m} = \frac{R_{m,next}}{1 + x_{O_2,m}}\]
It should be noted, however, that because the muscle resistance is also controlled by the sympathetic response, the resistance against which the autoregulation acts is that determined by Equation 26.
TBI
Traumatic brain injuries are relatively common, affecting millions annually. They are usually defined as a blunt or penetrating injury to the head that disrupts normal brain function. Furthermore, they are classified as either focal (e.g. cerebral contusions, lacerations, and hematomas) or diffuse (e.g. concussions and diffuse axonal injuries) [2]. The scope of the BioGears TBI model is somewhat limited by the low fidelity of the modeled brain. The brain is represented in the current BioGears Cardiovascular circuit with only two resistors and a compliance, all within one compartment. Because the circuit is modeled in this way, TBI is considered as an acute, non-localized, non-penetrating injury from a circuit perspective. Thus, the TBI model can account for intracranial pressure and cerebral blood flow on the basis of the whole brain, but not to specific areas of the brain. However, BioGears does provide for three injury inputs: diffuse, right focal, and left focal. Similarly to the Renal System, the BioGears brain circuit could be expanded to accommodate a higher-fidelity brain model.
Three important metrics are used to evaluate patients with traumatic brain injuries: intracranial pressure (ICP), cerebral blood flow (CBF), and cerebral perfusion pressure (CPP). Patients with brain injuries often exhibit increased intracranial pressure, decreased cerebral blood flow, and a cerebral perfusion pressure outside of a normal range [336]. Cerebral perfusion pressure is defined as
\[ CPP = MAP - ICP \]
Where MAP is the mean arterial pressure. In order to model these behaviors, the Brain Injury action in BioGears will modify the resistors of the brain circuit, which is shown in Figure 5 below. The brain circuit is a section of the cardiovascular circuit.
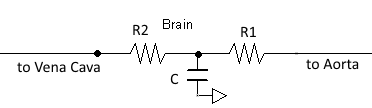
By increasing R1 and R2, the ICP can be increased while CBF decreases. The resistors are tuned based on the severity (on a scale from 0 to 1) of TBI such that ICP is above 25 mmHg and CBF is near 8 mL per 100 grams of brain tissue per minute for the most severe injury.
Pupillary Response
The pupil's diameter is controlled by the autonomic nervous system in order to affect the amount of light entering the eye. This diameter control is carried out by two muscles: the pupilloconstrictor, which is parasympathetically controlled (via the neurotransmitter acetylcholine), and the pupillodilator, which is sympathetically controlled (via the neurotransmitter norepinephrine) [2]. The synaptic pathways for these two pupil effects differ, and thus, any deviation from normal pupil behavior can shed light on any interference, whether that be a brain injury causing increased pressure on a nerve or a drug effect interfering with synaptic transmission. Because pupil examination is informative yet minimally invasive, it is an excellent tool for helping to diagnose neurological problems. The PERRLA assessment is commonly used to classify pupillary behavior: Pupils Equal, Round, Reactive to Light, and Accomodating. Pupillary response in BioGears is modeled by tracking any modification to pupil size and light reactivity for each eye. Both TBI actions and drugs can apply modifiers to pupil size and reactivity.
Pupil size and reactivity can vary patient-to-patient based on many factors, including age, mental and emotional state, and ambient light conditions [396]. Furthermore, pupillary assessments like PERRLA are often qualitative rather than quantitative. Because of this, BioGears models pupillary modifiers rather than discrete pupil sizes and size changes over time. In this way, the pupillary effects can be assessed qualitatively without the need for baseline patient values for pupil size and reactivity.
There are two ways to affect the pupils in BioGears: drug pharmacodynamic effects and TBI. For a discussion of pharmacodynamic effects on pupillary response, see Drugs Methodology. The other method of influencing pupillary response is TBI. Increasing intracranial pressures constrict ocular nerves, causing pupillary disruptions [164]. Because of this relationship between ICP and pupil effects, ICP is the metric on which pupillary modifiers are based. For the pupil size modifier, Equation 9 was developed so that pupil size (ms) begins to see effects when ICP increases above around 20 mmHg, the pressure at which recoverable brain damage is often observed [336], hitting its maximum slope at 22.5 mmHg, and leveling off as ICP approaches 25 mmHg. For pupil light reactivity (mr), the curve seen in Equation 10 was developed so that it remains at 0 until ICP approaches 20 mmHg, then drops off sharply towards -1 as ICP approaches 25 mmHg. For both of these modifiers, a 1 represents "maximal" effect, -1 represents "minimal" effect, and 0 represents no effect. So a pupil size modifier of 1 would mean the pupil size is at its maximum possible diameter.
\[m_s=1/(1+(e^{-2.3\left(ICP-22.5\right)})\]
\[m_{r} =-.001*10^{.3(ICP-15)} \]
For diffuse injuries, these modifiers are applied to both eyes. For focal injuries, the modifiers are applied to the eye on the same side as the injury, as this reflects the most common observed behavior [164].
Sleep Effects
We adapt the work of [312] and quantifies the effects of sleep deprivation through evolution of biological debt on the patient. We let biological debt be a function of metabolic demands that change based upon the amount of sleep the patient has had. A normal range of sleep throughout a simulation (6-9 hours a night) will show no noticable physiological signs on the patient. The evolution of the sleep debt equations are characterized by the following equations:
\[a(t) = \left( {\frac{{{L_1}}}{{\left( {1 + {e^{ - k({S_r}(t) - s)}}} \right)}}} \right) + {L_0}\]
\[c(t) = 5.1 - a(t)\sin \left( {\left( {\frac{\pi }{{48}}} \right)t} \right) \]
\[\frac{{dB}}{{dt}} = {p_w}{r_{wt}} + {p_{b1}}{r_{bt}}B(t) - {r_{bt}}x(t) \]
\[x(t) = c(t)\left( {\frac{{B(t)}}{{1 + B{{(t)}^2}}}} \right). \]
Here Sr(t) is the ratio between total sleep and wake times over the simulation period. In general, a patient begins with 8 hours of sleep. The amount of sleep a patient has had over the previous 24 hours can be set in the patient xml. This allows for sleep deprived patients to be loaded into BioGears without the need to run a simulation for a long period of time. equations 11 and 12 define the circadian rhythm burden on the patient and are scaled as a function of how much sleep the patient has had. equation 13 defines how the biological debt evolves over time. The parameters in the ODE are defined to be: pw = Price of expending energy while awake, rw= rate of energy to waking effort, rb = rates of energy to biological investment, Pb1 = come scaling factor that relates price of using energy while awake.
Patient Variability
The baroreceptor reflex gains and time constants are independent of patient configuration. However, set-points are computed after stabilization, and the baroreceptor reflex drives towards a configuration-specific homeostasis. Because TBI uses multiplicative factors to modify the brain section of the cardiovascular circuit, the patient variability of TBI is the same as that seen in the Cardiovascular System. There is no patient variability inherent in BioGears pupillary response model, as it uses modifiers instead of baseline values. A detailed discussion of patient configuration and variability in BioGears is available in the Patient Methodology report.
Dependencies
The baroreceptors interact directly with the cardiovascular system by modifying cardiovascular circuit and heart driver parameters. These include heart rate, left and right heart elastance, systemic vascular resistance and systemic vascular compliance. The cardiovascular parameters are modified by first calculating the normalized change in the parameter. This normalized change is passed into the common data model (CDM) where the cardiovascular system may extract the change and then apply it locally as a fractional adjustment. The resultant hemodynamic changes feedback directly to the MAP, and the updated MAP is used by the Nervous system in the next time slice to compute new normalized baroreceptor effects. TBI also directly modifies the cardiovascular circuit, specifically both the upstream and downstream brain resistors. Finally, the Drugs system can contribute additional pupillary effects, that combine with possible TBI pupil effects via simple summation.
Assumptions and Limitations
The current implementation of the baroreceptor model does not track adjustments in unstressed volume. Currently BioGears does not correctly represent the physiologic unstressed volume under resting conditions. Therefore, these changes to the unstressed volume cannot be reflected in the BioGears engine. This may be addressed in future releases of the engine.
The BioGears TBI model assumes an acute injury to the brain; chronic effects are not considered, and neither are consciousness assessments. The brain is considered to be one compartment and is not subdivided into discrete functional areas. This means that there is no circuit distinction between a diffuse TBI and a Left Focal TBI. The only difference between the TBI actions is the expected pupil effect. TBI metric validation assumes a supine adult. The current TBI model does not consider specific effects of CO2 saturation, O2 saturation, or blood pH on CBF.
Actions
Insults
Pain Stimulus
The Pain Stimulus action triggers changes to the cardiovascular, respiratory, and endocrine systems that are associated with sympathetic activation. Action initiation requires a severity (0-1 scale) and a location. If multiple locations are specified, the pain severities are summed until the upper boundary of 1 is reached. The severity is assumed to correspond directly to the Visual Analog Scale (VAS) used to quantify pain in clinical settings (e.g. Pain Severity = 0.5 –> VAS = 5). To account for the fact that individuals perceive pain differently, a Pain Susceptibility parameter was added to the BioGears patient definition. This modifier has a range of -1 to 1, with positive values implying heightened sensitivity to pain and negative values indicating blunted sensitivity. If not susceptibility is set in the patient file, then a value of 0 is assumed (i.e. "average susceptibility). The susceptibility parameter is added to the pain severity when a stimulus action is applied. For example, when exposed to a pain stimulus with a severity of 0.5, two patients with pain susceptibilities of -0.1 and 0.2 would report respective pain levels of 0.4 and 0.7 (4 and 7 on the Visual Analog Scale).
The pain scale calculated from the action severity and patient susceptibility is used to establish changes in physiology. Heart rate, respiration rate, and blood pressure all increase as the consolidated pain scale increases. Much of this response is achieved by increasing production of epinephrine in the BioGears Endocrine system. Administration of analgesic drugs (such as Morphine or Fentanyl) lowers the pain score and reverses these physiological trends.
Brain Injury
The Brain Injury action refers to an acute injury to the brain. Whereas in a real patient, a TBI could have manifold effects, both acute and chronic, BioGears only considers the effects of TBI on brain vascular resistance and pupillary response. The effects of the Brain Injury action depend on the severity value from 0 to 1 and a Type (Diffuse, Left Focal, or Right Focal) assigned to the injury. A severity of 0 will result in a multiplicative factor of 1 being applied to both the upstream and downstream resistors in the brain, which equates to no deviation from the normal, uninjured state. For an injury severity of 1, the upstream resistor is assigned a multiplicative factor of 4.775 and the downstream resistor is assigned a multiplicative factor of 30.409. Severity values between 0 and 1 are converted to multiplicative factors linearly. Increased flow resistance results in increased ICP and decreased CBF. A Diffuse-type injury affects both eyes equally, whereas a Left Focal injury affects only the left eye, and a Right Focal injury affects only the right eye.
Events
Intracranial Hypertension
Intracranial Hypertension is triggered when the intracranial pressure exceeds 25 mmHg. The event is reversed when the pressure returns below 24 mmHg.
Intracranial Hypertension
Intracranial Hypotension is triggered when the intracranial pressure drops below 7 mmHg. The event is reversed when the pressure returns above 7.5 mmHg.
Results and Conclusions
Validation - Resting Physiologic State
No resting state physiology validation was completed, because the baroreceptors do not provide feedback during the initial resting and chronic stabilization phases. For more information on the stabilization phases, see System Methodology.
Validation - Actions and Conditions
Baroreceptor Reflex
The baroreceptor reflex is validated through simulation of an acute hemorrhage scenario. This scenario begins with the healthy male patient. After a short time a massive hemorrhage (bleeding rate of ~1000 mL/min) is initiated, and after 30 seconds the bleeding is stopped. The responses for cardiac output, heart rate, systemic vascular resistance and blood volume are shown in Figure 6. The responses shown in the plot are initially driven by decreasing blood volume, resulting in decreased preload and a subsequent reduction in cardiac output. The baroreceptors attempt to maintain the arterial pressure by increasing the heart rate and contractility, increasing the systemic vascular resistance, and reducing vascular compliance. For this specific hemorrhage scenario, there is an expected 30% increase in heart rate, 15-20% decrease in cardiac output, and 10-15% increase in systemic vascular resistance [136]. BioGears baroreceptor feedback does a fair job reaching these values, though it is a bit aggressive in doing so. The heart rate increase observed is much higher than expected, but the changes in cardiac output and systemic vascular resistance are in line with expectations. The validation results are shown in tabular form below. Additional validation related to the baraoreceptor reflex and hemodynamic stability can be found in the Cardiovascular Methodology report.
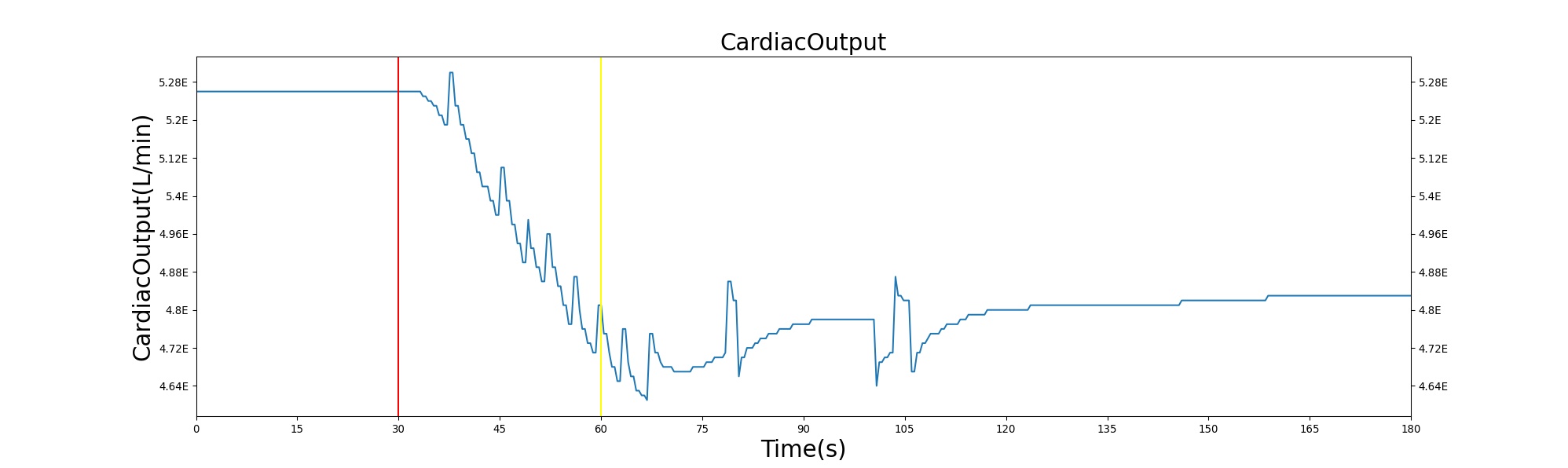
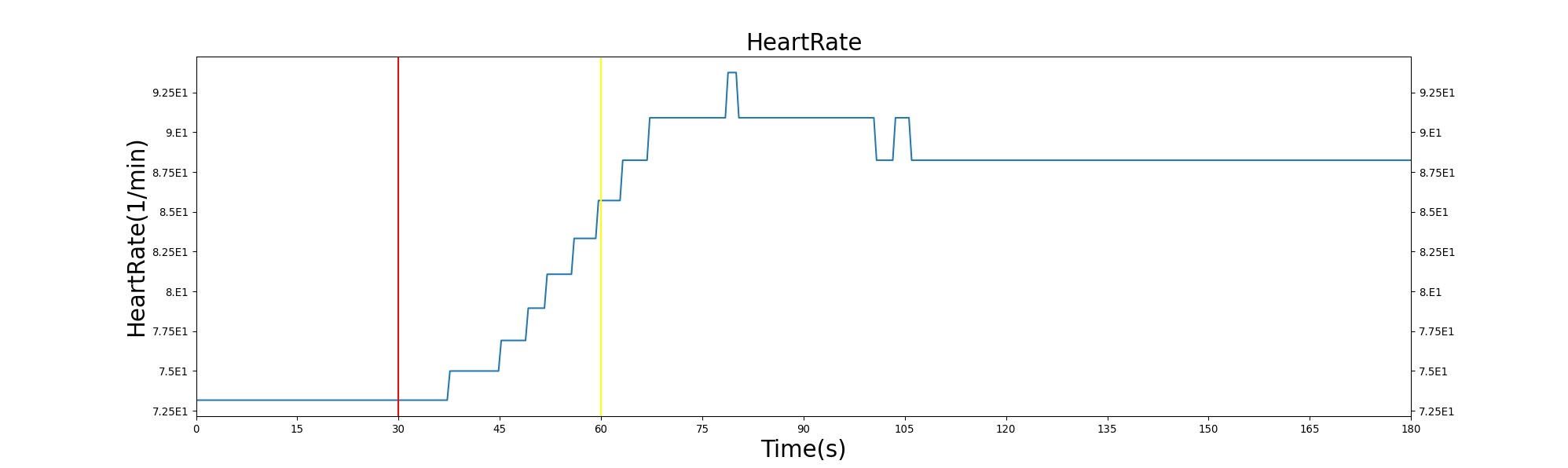
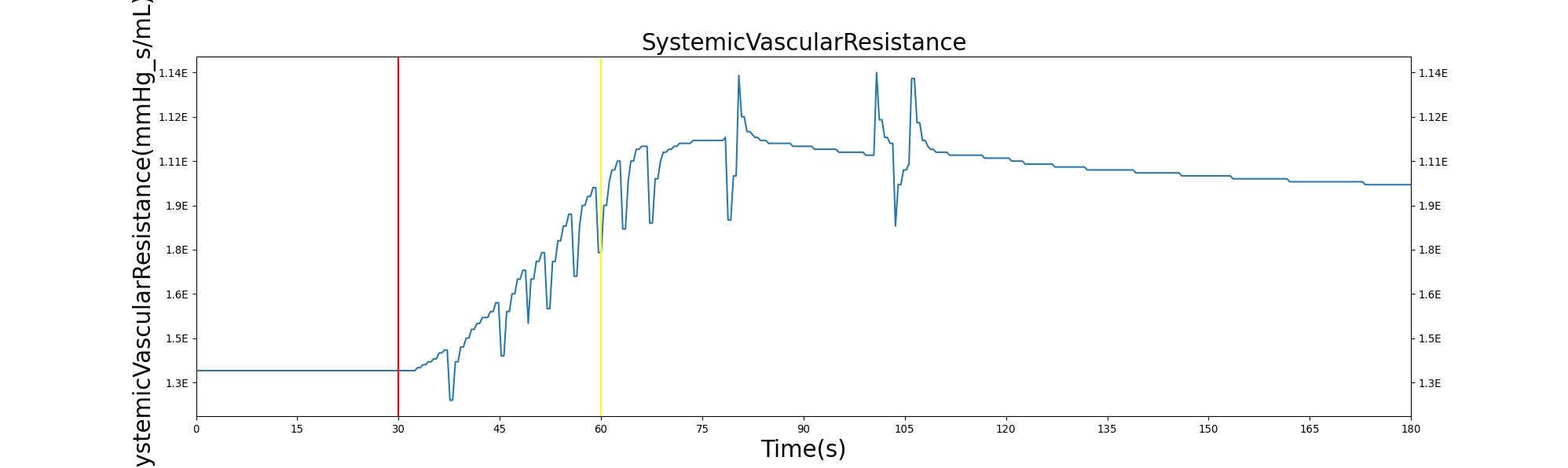

Table 1. The cardiac output, heart rate, systemic vascular resistance and blood volume are shown as a function of time for the acute hemorrhage scenario. There is a noticeable decrease in blood volume and cardiac output due to the fluid loss. The baroreceptor response in this situation leads to an increase in heart rate and systemic vascular resistance in an attempt to maintain arterial pressure.
| Action | Notes | Sampled Scenario Time (s) | Heart Rate (beats/min) | Cardiac Output (mL/min) | Systemic Vascular Resistance (mmHg s/mL) |
|---|---|---|---|---|---|
| Hemorrhage | 10% blood loss in 30 s | 325 | Increase ~30% [136] [251] | Decrease ~15-20% [136] [251] | Increase 10-15% [136] [251] |
Chemoreceptor Reflex
The performance of the Chemoreceptor model in BioGears was validated under both hypercanpic and hypoxic conditions. Hypercapnic validation was based on the study of Reynolds, Milhorn, and Holloman [277], in which healthy volunteers breathed air with supernormal carbon dioxide levels (3%, 5%, 6%, and 7% CO2). Likewise, hypoxic validation scenarios used data from Reynolds and Milhorn [276]. Volunteers in this study breathed 7%, 8%, and 9% O2 in nitrogen.
Brain Injury
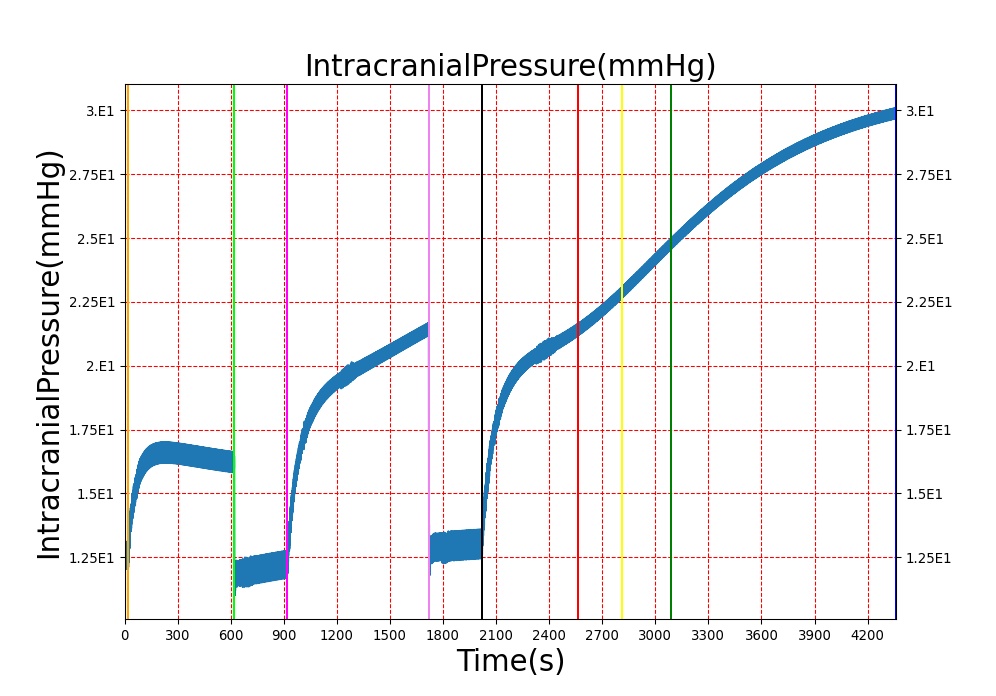
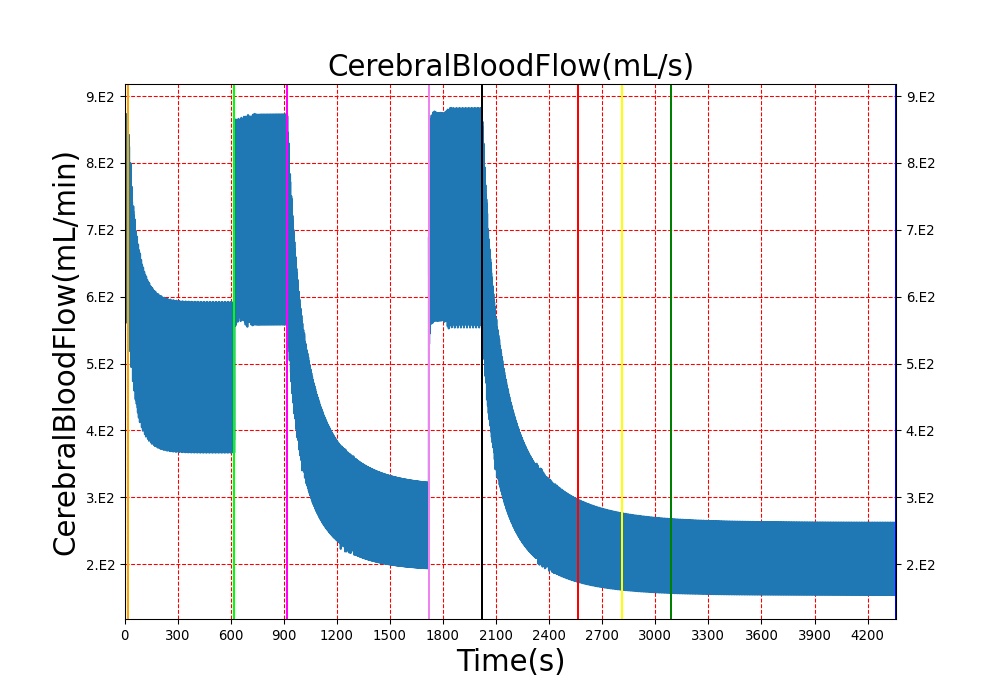
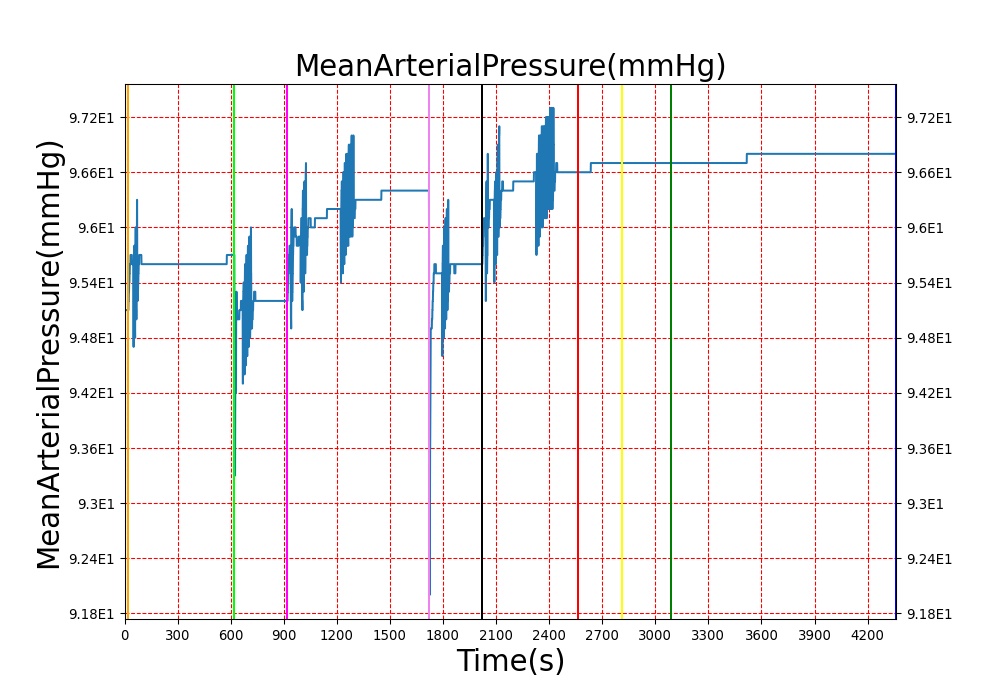
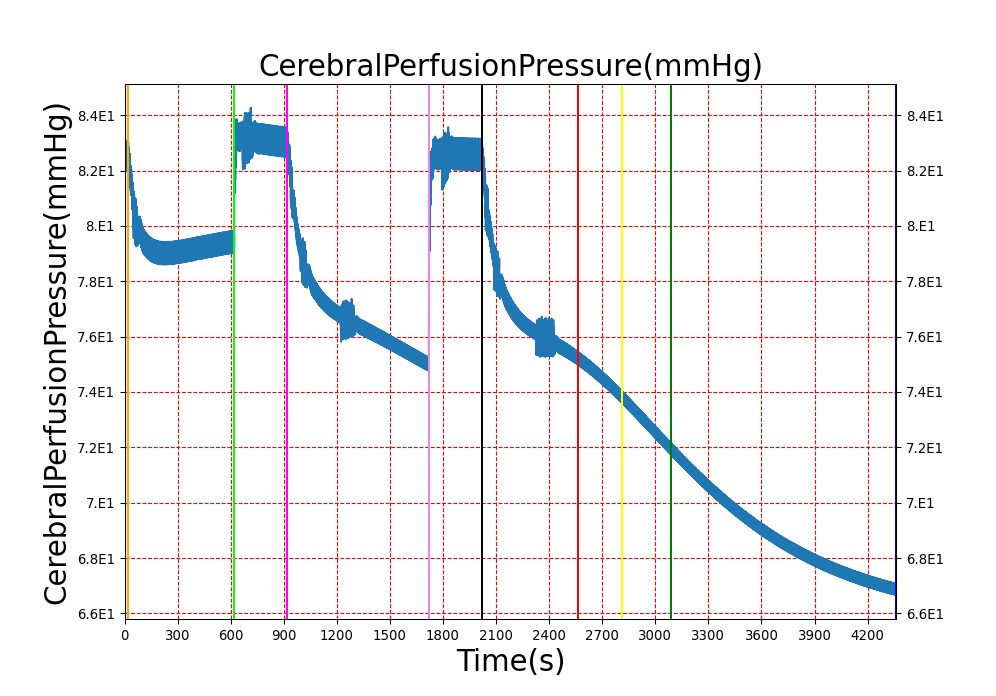
The Brain Injury action is validated through repeated application and removal of increasing severities of TBI. The scenario begins with a healthy male patient. After a short time, a mild brain injury (Severity = 0.2, Type = Diffuse) is applied, and the patient is allowed to stabilize before the injury state is removed (only one TBI action can be in effect at a time, so adding a Diffuse Severity 0 TBI removes all TBI effects). This process is repeated for a more severe injury (Severity = 0.75, Type = Left Focal) and severe (Severity = 1, Type = Right Focal) brain injury. We expect to see increases in ICP, with the most severe injury resulting in an ICP greater than 25 mmHg and decreases in CBF, with the most severe case approaching 8 mL per 100 grams of brain per minute (108 mL per minute for the validated patient) [216] [336]. The scenario shows good agreement for these values, and the patient even dies after some time with the most severe injury. We expect CPP to either increase above its maximum normal value or decrease below its minimum normal value, but, though we see a drop, it isn't quite as pronounced as expected [336]. We can also see that for the low severity injury, ICP doesn't quite reach the threshold to strongly affect the pupils. For the Left Focal injury, only the left pupil is affected, and for the Right Focal injury, only the right pupil is affected.
| 
|
| 
|

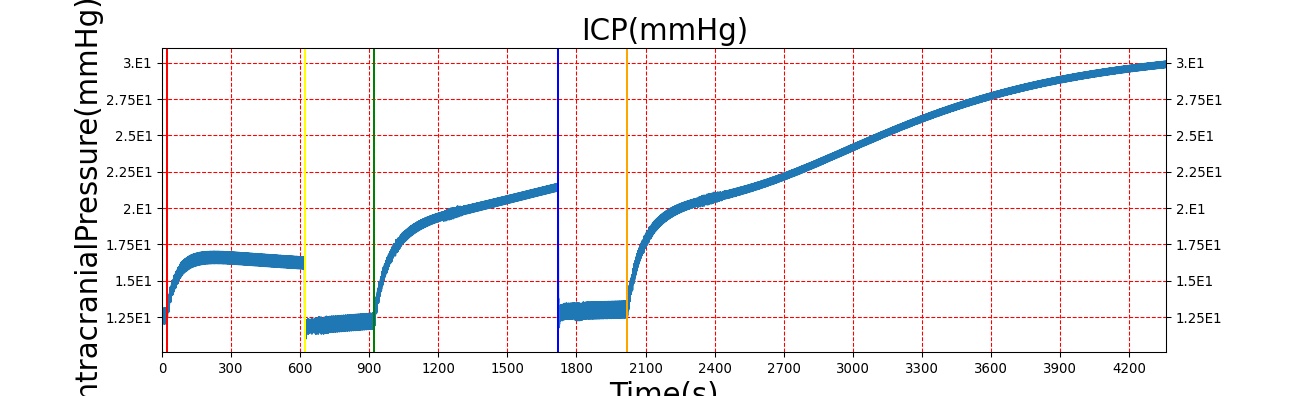
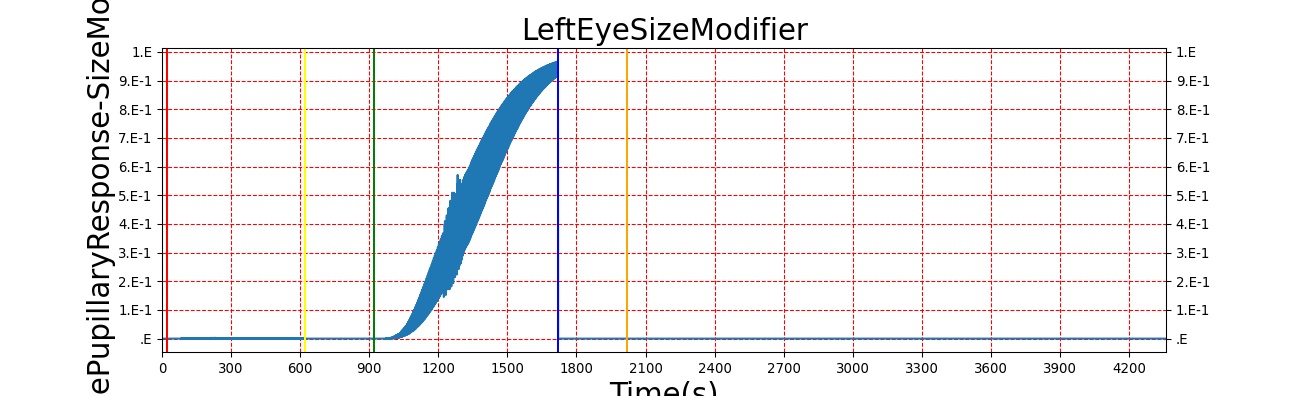
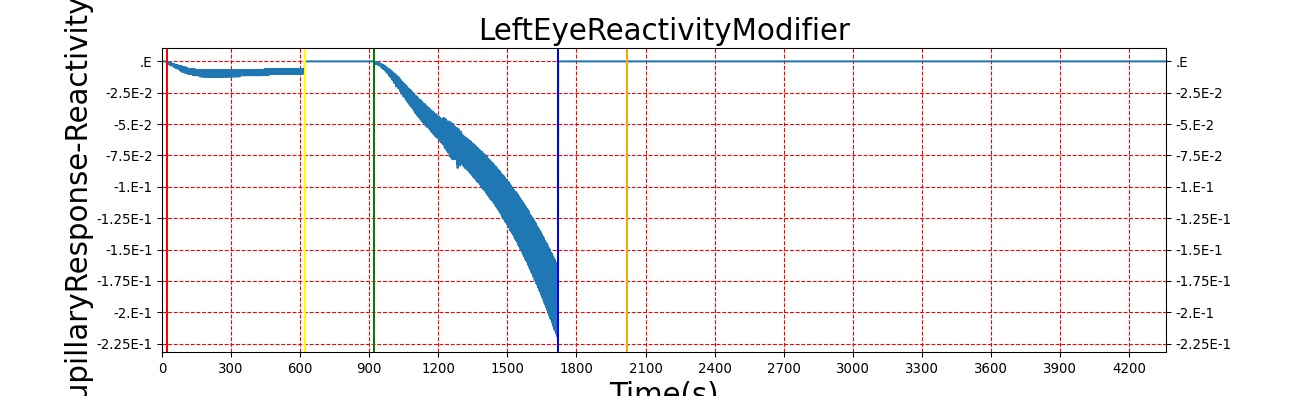
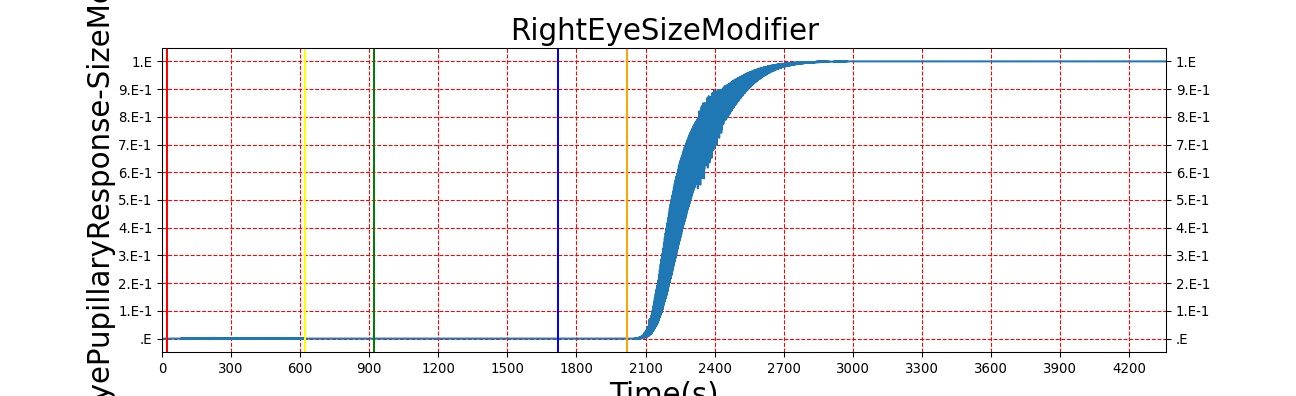
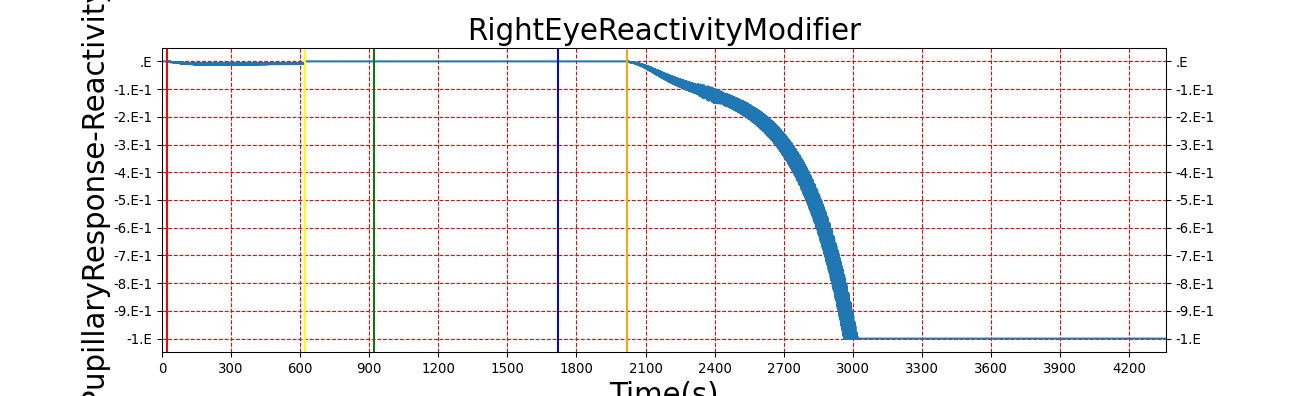

Table 2. The validation data for the TBI scenario shows good agreement with expected results.
| Action | Notes | Action Occurrence Time (s) | Sampled Scenario Time (s) | Intracranial Pressure (mmHg) | Cerebral Blood Flow (mL/min) | Cerebral Perfusion Pressure (mmHg) | Heart Rate (1/min) | Respiration Rate (1/min) |
|---|---|---|---|---|---|---|---|---|
| Brain Injury | Severity 0.2, CPP=MAP-ICP, StandardMale brain mass=1450g | 20 | 600 | 10% Increase [216] | Decrease [336] | Decrease [18] | 0-10% Decrease [216] | 0-10% Decrease [216] |
| Brain Injury | Severity 0 | 620 | 900 | 7-15 mmHg [336] | 50-65 mL/100g/min [134] | 60-98 mmHg | 72 [134] | [12.0, 20.0], [13.0, 19.0] [325] [205] |
| Brain Injury | Severity 0.75 | 920 | 1700 | Increase [336] | Decrease [336] | Decrease [18] | 0-15% Decrease [216] | 0-20% Decrease [216] |
| Brain Injury | Severity 0 | 1720 | 2000 | 7-15 mmHg [336] | 50-65 mL/100g/min [134] | 60-98 mmHg | 72 [134] | [12.0, 20.0], [13.0, 19.0] [325] [205] |
| Brain Injury | Severity 1 | 2020 | 3220 | >25 mmHg [336] | <8 mL/100g/min [336] | Decrease [18] | Decrease [216] | Decrease [216] |
Sleep Deprivation
The sleep model in BioGears is validated through by running a patient through a sleep deprivation study that quantifies the patients response to meals and measures blood glucose and insulin synthesis [331]. We create a study that parallels the methods used in Speigel by creating patients who are restricted in their sleep to just 4 hours a night over a three day period. We measure different physiological markers similar to the ones used in the study, table 3. Vigilance and attention lapse data is validated from [213]. The study performed by McHill was similar enough for us to validate all metrics with a single sleep deprivation study.
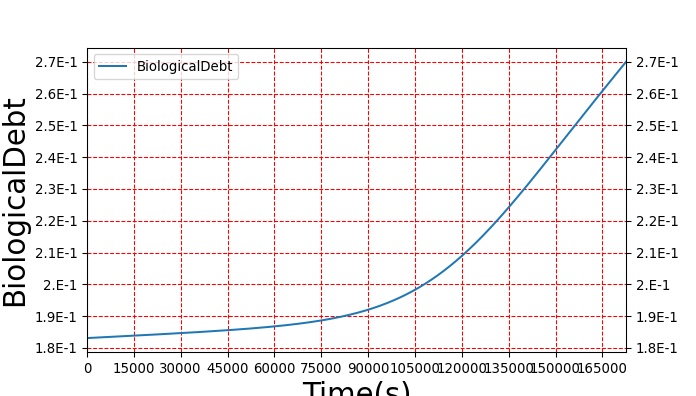

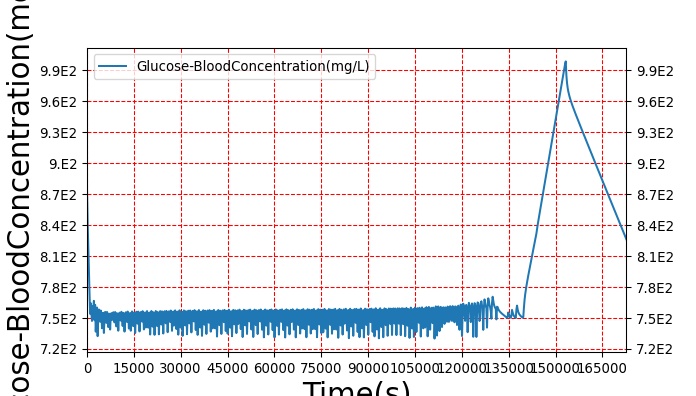
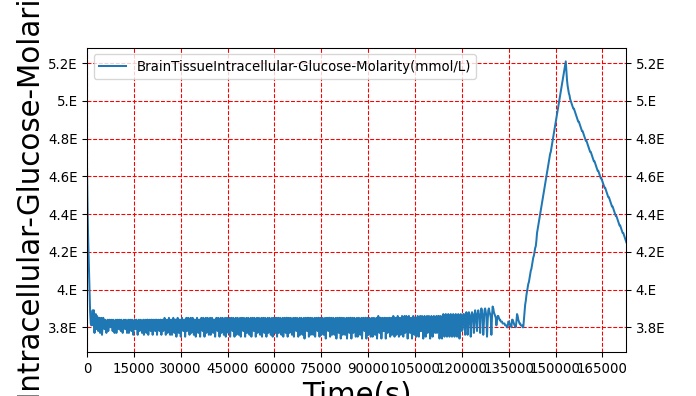
Table 3. The validation data for the sleep deprivation study shows good agreement with collected data.
Sleep
| Action | Notes | Sampled Scenario Time (min) | Glucose clearance (%/min) | Glucose effectiveness (%/min) clearance without insulin | Insulin response (pmol/min) | Stanford sleepyness score (unitless) | Cerebral glucose uptake (% from baseline) | Reaction Time (ms) | Attention Lapses (% from baseline) |
|---|---|---|---|---|---|---|---|---|---|
| Sleep of 4hr per day for 5 days | sleep deprivation study taken from spiegle and McHill, given carb rich meal (62%) every 5h | 7200 | 40% lower (1.42%/min compared to 2.4%/min [331] | Decrease 30% [331] | Decrease from 432 to 304 pmol/min [331] | Increase from 2.1 to 4.4 [331] | Decrease of 7% [331] | Increase ~1000% [213] | Increase of 100% [213] |
Conclusions
The Nervous System is currently in a preliminary state that contains only a baroreceptor feedback model, basic TBI, and pupillary response. The baroreceptor feedback is used to control rapid changes in arterial pressure by adjusting heart rate, heart elastance, and vascular resistance and compliance. The baroreceptor model has been validated by comparing the BioGears outputs to experimental data for hemorrhage. It currently shows good agreement with the expected trends, but the magnitude of the response is not a strong as the validation data. This is due to a large total vascular compliance, which allows for large changes in blood volume with small changes in pressure. Future adjustments to the cardiovascular circuit would correct the vascular compliance and improve the accuracy of the model. The TBI model shows good agreement for the most prominent TBI metrics, ICP and CBF, for acute brain injuries. Pupillary response behaves as expected and arms BioGears with yet another tool for matching output with clinical data.
Future Work
Coming Soon
- Chemoreceptor modification of heart contractility
- Local autoregulation
- Improved sympathetic and parasympathetic control
Recommended Improvements
- Including unstressed volume in the tone model
- Patient variability incorporated into the baroreceptor reflex model constants
- Positional variability
- Higher-fidelity brain model with localized injuries
- Interventions to treat TBI like drainage of cerebrospinal fluid, hypothermic treatment, hyperventilation, and mannitol therapy
- Consciousness model, including reduced level of consciousness with carbon monoxide and other intoxications
- Sleep
- Heart rate and respiration rate effects from TBI
Appendices
Acronyms
CBF - Cerebral Blood Flow
CNS - Central Nervous System
CPP - Cerebral Perfusion Pressure
ICP - Intracranial Pressure
PERRLA - Pupils Equal, Round, Reactive to Light, and Accommodating
PNS - Peripheral Nervous System
MAP - Mean Arterial Pressure
mmHg - Millimeters mercury
Data Model Implementation
Nervous





